
【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
【答案】水面上涨到与抛物线拱顶距2米时,小船开始不能通行
【解析】
试题分析:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0).将B(4,-5)代入得p=1.6,所以x2=-3.2y,当船两侧与抛物线接触时不能通过,由此能求出结果
试题解析:建立平面直角坐标系,

设拱桥型抛物线方程为x2=-2py(p>0).…(2分)
将B(4,-5)代入得p=1.6,
∴x2=-3.2y,…(6分)
当船两侧与抛物线接触时不能通过,
设点A(2,yA),
由22=-3.2 yA,
得yA =-1.25,…(10分)
因为船露出水面的部分高0.75米,…(12分)
所以h=|yA|+0.75=2米.…(14分)
答:水面上涨到与抛物线拱顶距2米时,小船开始不能通行.…(16分)


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=2x-3-1的图象,只需把函数y=2x的图象上所有的点( )
A. 向右平移3个单位长度,再向下平移1个单位长度
B. 向左平移3个单位长度,再向下平移1个单位长度
C. 向右平移3个单位长度,再向上平移1个单位长度
D. 向左平移3个单位长度,再向上平移1个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
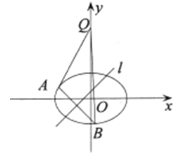
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,分别求满足下列条件的a,b值
(1)l1⊥l2,且直线l1过点(﹣3,﹣1);
(2)l1∥l2,且直线l1在两坐标轴上的截距相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
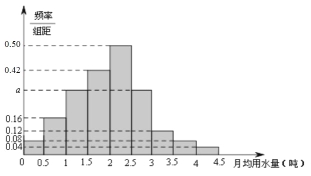
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
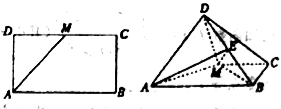
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,三棱锥
在何位置时,三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积之比为1:3?
的体积之比为1:3?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com