
已知二次函数 的导函数的图像与直线
的导函数的图像与直线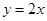 平行,且
平行,且 在
在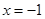 处取得极小值
处取得极小值 .设
.设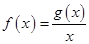 .
.
(1)若曲线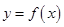 上的点
上的点 到点
到点 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
(1) 或
或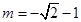 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)先设点 的坐标,利用两点间的距离公式将
的坐标,利用两点间的距离公式将 表示为
表示为 为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出
为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出 的值;(2)令
的值;(2)令 ,将函数
,将函数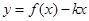 的零点转化为求方程
的零点转化为求方程 的根,对首项系数
的根,对首项系数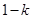 的符号进行分类讨论,以及在首项系数不为零时对
的符号进行分类讨论,以及在首项系数不为零时对 的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
试题解析:(1)依题可设 (
(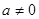 ),则
),则 ;
;
又 的图像与直线
的图像与直线 平行
平行 
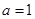
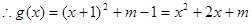 ,
,
 ,
,
设 ,则
,则

当且仅当 时,
时, 取得最小值,即
取得最小值,即 取得最小值
取得最小值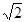
当 时,
时, 解得
解得
当 时,
时,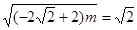 解得
解得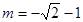
(2)由 (
( ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当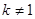 时,方程
时,方程 有二解
有二解 ,
,
若 ,
,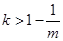 ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
当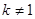 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当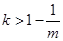 (
( ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点 .
.
考点:1.两点间的距离公式;2.基本不等式;3.分类讨论;4.一元二次方程的求解


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
(2009年广东卷文)(本小题满分14分)
已知二次函数![]() 的导函数的图像与直线
的导函数的图像与直线![]() 平行,且
平行,且![]() 在
在![]() =-1处取得最小值m-1(m
=-1处取得最小值m-1(m![]() ).设函数
).设函数![]()
(1)若曲线![]() 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为![]() ,求m的值
,求m的值
(2) ![]() 如何取值时,函数
如何取值时,函数![]() 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知二次函数![]() 的导函数的图像与直线
的导函数的图像与直线![]() 平行,且
平行,且![]() 在
在![]() =-1处取得最小值m-1(m
=-1处取得最小值m-1(m![]() ).设函数
).设函数![]() (1)若曲线
(1)若曲线![]() 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为![]() ,求m的值(2)
,求m的值(2) ![]() 如何取值时,函数
如何取值时,函数![]() 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源:2013届福建安溪梧桐中学、俊民中学高二下期末文科数学试卷(解析版) 题型:选择题
.已知二次函数 的导函数为
的导函数为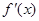 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则 的最小值为 ( )
的最小值为 ( )
A.2 B. C.3 D.
C.3 D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省卢氏一高高三适应性考试理科数学 题型:选择题
已知二次函数 的导函数为
的导函数为 ,
,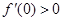 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则 的最小值为( )
的最小值为( )
A.2 B. C.3 D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省东至县高三一模理科数学试卷 题型:选择题
已知二次函数 的导函数为
的导函数为 ,
,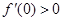 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则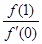 的最小值为 ( )
的最小值为 ( )
A. 2 B.3/2 C. 3 D.5/2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com