
【题目】已知点F1、F2为双曲线C:x2﹣ ![]() =1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
=1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2 , 求 ![]() 的值.
的值.
【答案】
(1)解:设F2,M的坐标分别为 ![]() ,
,
因为点M在双曲线C上,所以 ![]() ,即
,即 ![]() ,所以
,所以 ![]() ,
,
在Rt△MF2F1中,∠MF1F2=30°, ![]() ,所以
,所以 ![]()
由双曲线的定义可知: ![]()
故双曲线C的方程为: ![]()
(2)解:由条件可知:两条渐近线分别为 ![]()
设双曲线C上的点Q(x0,y0),设两渐近线的夹角为θ,
则点Q到两条渐近线的距离分别为 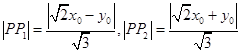 ,
,
因为Q(x0,y0)在双曲线C: ![]() 上,
上,
所以 ![]() ,又cosθ=﹣
,又cosθ=﹣ ![]() ,
,
所以 ![]() =﹣
=﹣ 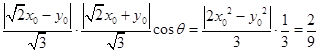
【解析】(1)设F2 , M的坐标分别为 ![]() ,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得
,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得 ![]() ,利用向量的数量积公式,即可求
,利用向量的数量积公式,即可求 ![]() 的值.
的值.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足 ![]() ,若n∈N*时,anbn+1﹣bn+1=nbn .
,若n∈N*时,anbn+1﹣bn+1=nbn .
(Ⅰ)求{bn}的通项公式;
(Ⅱ)设cn=anbn , 求{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1 , F2分别是椭圆C: ![]() =1(a>b>0)的左、右焦点,且焦距为2
=1(a>b>0)的左、右焦点,且焦距为2 ![]() ,动弦AB平行于x轴,且|F1A|+|F1B|=4.
,动弦AB平行于x轴,且|F1A|+|F1B|=4.
(1)求椭圆C的方程;
(2)若点P是椭圆C上异于点 ![]() 、A,B的任意一点,且直线PA、PB分别与y轴交于点M、N,若MF2、NF2的斜率分别为k1、k2 , 求证:k1k2是定值.
、A,B的任意一点,且直线PA、PB分别与y轴交于点M、N,若MF2、NF2的斜率分别为k1、k2 , 求证:k1k2是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义f(x)={x}(其中{x}表示不小于x的最小整数)为“取上整函数”,例如{2.1}=3,{4}=4.以下关于“取上整函数”性质的描述,正确的是( ) ①f(2x)=2f(x);
②若f(x1)=f(x2),则x1﹣x2<1;
③任意x1 , x2∈R,f(x1+x2)≤f(x1)+f(x2);
④ ![]() .
.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心为原点O,F(﹣2 ![]() ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( ) 
A.![]() =1
=1
B.![]() =1
=1
C.![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)已知集合X={1,2,3},Yn={1,2,3...,n}(n![]() N*),Sn={(a,b)|a整除b或b整除a, a
N*),Sn={(a,b)|a整除b或b整除a, a![]() X, b
X, b![]() Yn}, 令f(n)表示集合Sn所包含元素的个数。
Yn}, 令f(n)表示集合Sn所包含元素的个数。
(1)写出f(6)的值;
(2)当n≥6时,写出f(n)的表达式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2. 
(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)若二面角B﹣AB1﹣C1的余弦值为 ![]() ,求斜三棱柱ABC﹣A1B1C1的高.
,求斜三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手.从这7名队员中随机选派4名队员参加第一阶段的比赛.
(1)求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
(2)设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com