
【题目】已知函数f(x)=x2﹣2x﹣2
(Ⅰ)用定义法证明:函数f(x)在区间(﹣∞,1]上是减函数;
(Ⅱ)若函数g(x)=f(x)﹣mx是偶函数,求m的值.
【答案】解:(Ⅰ)设﹣∞<x1<x2≤1,
所以,f(x1)﹣f(x2)=( ![]() ﹣2x1﹣2)﹣(
﹣2x1﹣2)﹣( ![]() ﹣2x2﹣2)=(x1﹣x2 )(x1+x2﹣2),
﹣2x2﹣2)=(x1﹣x2 )(x1+x2﹣2),
因为﹣∞<x1<x2,所以,x1﹣x2<0,x1+x2﹣2<0,
所以,f(x1)﹣f(x2)>0,
所以,f(x1)>f(x2),
所以函数f(x)在区间(﹣∞,1]上是减函数.
(Ⅱ)因为函数g(x)=f(x)﹣mx=x2﹣(2+m)x﹣2,
又因为g(x)是偶函数,2+m=0,
∴m=﹣2.
【解析】(1)根据定义法进行设值作差变形整理可得,(2)当g(x)为偶函数时,其二次函数的对称轴为y轴,即2+m=0,即可解得m=-2.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质和二次函数在闭区间上的最值的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①mn=nm类比得到ab=ba;
②(m+n)t=mt+nt类比得到(a+b)c=ac+bc;
③(mn)t=m(nt) 类比得到(ab)c=a(bc);
④t≠0,mt=rtm=r类比得到p≠0,ap=bpa=b;
⑤|mn|=|m||n|类比得到|ab|=|a||b|;
⑥ ![]() =
= ![]() 类比得到
类比得到 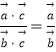 .
.
以上式子中,类比得到的结论正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=lnx
(1)若曲线h(x)=f(x)+ax2﹣ex(a∈R)在点(1,h(1))处的切线垂直于y轴,求函数h(x)的单调区间;
(2)若函数 ![]() 在区间(0,2)上无极值,求实数a的取值范围.
在区间(0,2)上无极值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 
(Ⅰ)求出f(5);
(Ⅱ)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E , F分别为AB , AD上的点,且 ![]() ,H , G分别为BC , CD的中点,则( )
,H , G分别为BC , CD的中点,则( )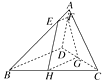
A.BD∥平面EFGH , 且四边形EFGH是平行四边形
B.EF∥平面BCD , 且四边形EFGH是梯形
C.HG∥平面ABD , 且四边形EFGH是平行四边形
D.EH∥平面ADC , 且四边形EFGH是梯形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com