
分析 (Ⅰ)可看出f(x)为奇函数,求f(x)的定义域为R,且容易得到f(-x)=-f(x),从而证出f(x)为奇函数;
(Ⅱ)由原不等式可以得到$\frac{6•{2}^{x}}{{2}^{2x}+1}>{2}^{x}$,可化简成22x<5,不等式两边取以2为底的对数便可得出实数x的取值范围.
解答 解:(Ⅰ)f(x)为奇函数,证明如下:
f(x)的定义域为R,f(-x)=$\frac{-6x}{{x}^{2}+1}=-f(x)$;
∴f(x)为奇函数;
(Ⅱ)由f(2x)>2x得,$\frac{6•{2}^{x}}{{2}^{2x}+1}>{2}^{x}$;
∴$\frac{6}{{2}^{2x}+1}>1$;
整理成22x<5;
∴2x<log25;
∴$x<\frac{lo{g}_{2}5}{2}$;
即$x<lo{g}_{2}\sqrt{5}$;
∴实数x的取值范围为(-∞,$lo{g}_{2}\sqrt{5}$).
点评 考查奇函数的定义及判断方法和过程,指数函数的值域,分式不等式的解法,以及指数式和对数式的互化,对数函数的单调性.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>1,x+$\frac{1}{x}$≤2 | B. | ?x>1,x+$\frac{1}{x}$≤2 | C. | ?x≤1,x+$\frac{1}{x}$≤2 | D. | ?x≤1,x+$\frac{1}{x}$≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
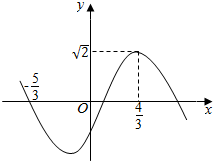 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com