
 =(cosα,(λ-1)sinα),
=(cosα,(λ-1)sinα), =(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且 与
与 互相垂直.
互相垂直. =
= ,tanβ=
,tanβ= ,求tanα的值.
,求tanα的值. •
• =
= -
- =cos2α+(λ-1)2sin2α-cos2β-sin2β=1-sin2α+(λ-1)2sin2α-1=(λ-1)2sin2α-sin2α;
=cos2α+(λ-1)2sin2α-cos2β-sin2β=1-sin2α+(λ-1)2sin2α-1=(λ-1)2sin2α-sin2α; 与
与 垂直,∴(λ-1)2sin2α-sin2α=0,即 λ(λ-2)sin2α=0,且0<α<π,∴sin2α≠0,
垂直,∴(λ-1)2sin2α-sin2α=0,即 λ(λ-2)sin2α=0,且0<α<π,∴sin2α≠0, 与
与 垂直时,
垂直时, =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),∴
=(cosβ,sinβ),∴ •
• =cosαcosβ+sinαsinβ=cos(α-β),
=cosαcosβ+sinαsinβ=cos(α-β), (0<α<β<π),即
(0<α<β<π),即 ,∴sin(α-β)=
,∴sin(α-β)=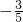 ,tan(α-β)=-
,tan(α-β)=- ,
, =
= =
=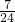 .
. ⊥
⊥ 得,(
得,( )•(
)•( )=0,代入数据计算,可求得λ的值;
)=0,代入数据计算,可求得λ的值; =
= ,可得cos(α-β),进而得sin(α-β),tan(α-β)的值,又知tanβ,
,可得cos(α-β),进而得sin(α-β),tan(α-β)的值,又知tanβ,

科目:高中数学 来源: 题型:
. | z1z2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
| a |
| b |
| c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com