
【题目】【2018届吉林省普通中学高三第二次调研】设椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,离心率为
,离心率为![]() ,短轴长为
,短轴长为![]() ,已知
,已知![]() 是抛物线
是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程和抛物线
的方程和抛物线![]() 的方程;
的方程;
(2)若抛物线![]() 的准线
的准线![]() 上两点
上两点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856284)
在△ABC中,角A,B,C的对边分别为a,b,c,已知c=b(1+2cosA).
(Ⅰ)求证:A=2B;
(Ⅱ)若a=![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且S1+a1,S3+a3,S2+a2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an+1=![]() ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856321)已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),则函数f(x)的单调增区间为( )
),则函数f(x)的单调增区间为( )

A. [-![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z) B. [
+2kπ](k∈Z) B. [![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
C. [-![]() +kπ,
+kπ, ![]() +kπ](k∈Z) D. [
+kπ](k∈Z) D. [![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856334)
已知函数f(x)=ln x+ax2+1.
(Ⅰ)当a=-1时,求函数f(x)的极值;
(Ⅱ)当a>0时,证明:存在正实数λ,使得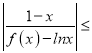 λ恒成立.
λ恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(m2-m-1)·![]() 是幂函数,对任意x1,x2∈(0,+∞)且x1≠x2,满足
是幂函数,对任意x1,x2∈(0,+∞)且x1≠x2,满足![]() ,若a,b∈R且a+b>0,ab<0,则f(a)+f(b)的值( )
,若a,b∈R且a+b>0,ab<0,则f(a)+f(b)的值( )
A. 恒大于0 B. 恒小于0
C. 等于0 D. 无法判断
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,与椭圆交于另一个点
,与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.
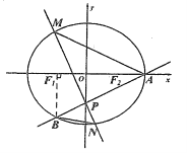
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点(
两点(![]() 不与
不与![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α外有两条直线m和n,如果m和n在平面α内的投影分别是m1和n1,给出下列四个命题:①m1⊥n1m⊥n;②m⊥nm1⊥n1;③m1与n1相交m与n相交或重合;④m1与n1平行m与n平行或重合.其中不正确的命题个数是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com