
已知函数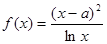 (其中
(其中 为常数).
为常数).
(Ⅰ)当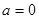 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ) 当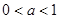 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且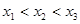 .
.
证明: .
.
(Ⅰ)单调减区间为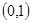 ,
,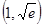 ;增区间为
;增区间为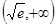 .
.
(Ⅱ)利用导数研究得到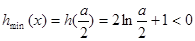 ,所以
,所以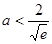 ,
,
当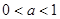 时,
时,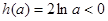 ,
,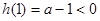 ,
,
∴ 函数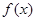 的递增区间有
的递增区间有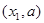 和
和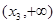 ,递减区间有
,递减区间有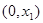 ,
, ,
,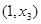 ,
,
此时,函数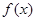 有3个极值点,且
有3个极值点,且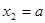 ;
;
当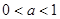 时,
时,
通过构造函数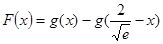 ,证得当
,证得当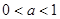 时,
时,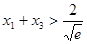 .
.
【解析】
试题分析:(Ⅰ) 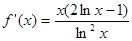
令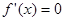 可得
可得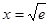 .列表如下:
.列表如下:
|
|
|
|
|
|
|
|
- |
- |
0 |
+ |
|
|
减 |
减 |
极小值 |
增 |
单调减区间为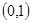 ,
,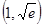 ;增区间为
;增区间为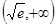 .
5分
.
5分
(Ⅱ)由题,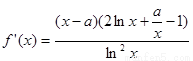
对于函数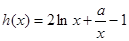 ,有
,有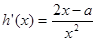
∴函数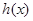 在
在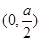 上单调递减,在
上单调递减,在 上单调递增
上单调递增
∵函数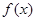 有3个极值点
有3个极值点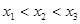 ,
,
从而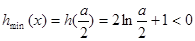 ,所以
,所以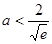 ,
,
当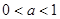 时,
时,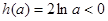 ,
,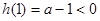 ,
,
∴ 函数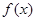 的递增区间有
的递增区间有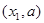 和
和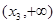 ,递减区间有
,递减区间有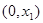 ,
, ,
,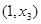 ,
,
此时,函数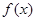 有3个极值点,且
有3个极值点,且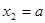 ;
;
∴当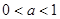 时,
时,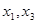 是函数
是函数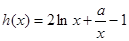 的两个零点, 9分
的两个零点, 9分
即有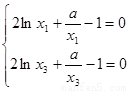 ,消去
,消去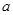 有
有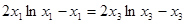
令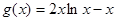 ,
,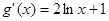 有零点
有零点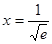 ,且
,且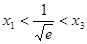
∴函数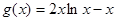 在
在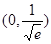 上递减,在
上递减,在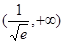 上递增
上递增
要证明 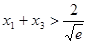
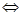
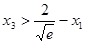
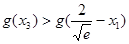
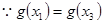
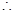 即证
即证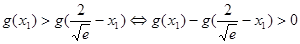
构造函数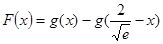 ,
,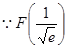 =0
=0
只需要证明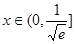 单调递减即可.而
单调递减即可.而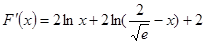 ,
,
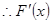 在
在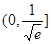 上单调递增,
上单调递增, 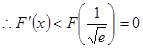
∴当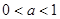 时,
时,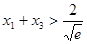 . 14分
. 14分
考点:本题主要考查应用导数研究函数的单调性及极值,不等式的证明。
点评:典型题,本题属于导数应用中的基本问题,像涉及恒成立问题,往往通过研究函数的最值达到解题目的。证明不等式问题,往往通过构造新函数,研究其单调性及最值,而达到目的。本题(II)难度较大。


科目:高中数学 来源:2013-2014学年安徽“江淮十校”协作体高三上学期第一次联考文数学卷(解析版) 题型:解答题
已知函数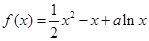 (其中
(其中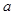 为常数).
为常数).
(I)当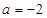 时,求函数
时,求函数 的最值;
的最值;
(Ⅱ)讨论函数 的单调性.
的单调性.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数 (其中
(其中 为常数).
为常数).
(Ⅰ)当 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)当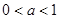 时,设函数
时,设函数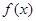 的3个极值点为
的3个极值点为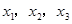 ,且
,且 .证明:
.证明: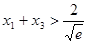 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市高三上学期期中考试数学卷 题型:解答题
(本题满分16分,第1小题5分,第2小题6分,第3小题5分)
已知函数 ,其中
,其中 为常数,且
为常数,且
(1)若 是奇函数,求
是奇函数,求 的取值集合A;
的取值集合A;
(2)(理)当 时,设
时,设 的反函数为
的反函数为 ,且函数
,且函数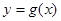 的图像与
的图像与 的图像关于
的图像关于 对称,求
对称,求 的取值集合B;
的取值集合B;
(文)当 时,求
时,求 的反函数;
的反函数;
(3)(理)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(文)对于问题(1)中的A,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com