解:(1)设点(-c,-y
0),Q(c,y
0),其中y
0>0,∵点P在椭圆C上,
∴
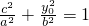
,
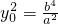
,

,
∴
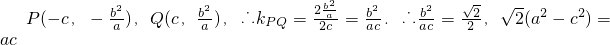
,
从而

,解得
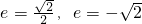
(舍去).
(2)由(1)知,
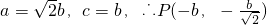
,
∴以PQ为直径的圆的方程为
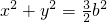
.
∵该圆与直线x+y+6=0相切,∴
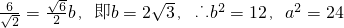
.
∴椭圆的标准方程为
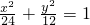
.
(3)由(1)知,

,故椭圆方程为
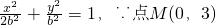
在椭圆内部,
∴b>3.
设N(x,y)为椭圆上任意一点,则MN
2=x
2+(y-3)
2=-(y+3)
2+2b
2+18,其中-b≤y≤b.∵b>3,
∴-b<-3,∴当y=-3时,MN
2取得最大值2b
2+18.
依题意:

,∴MN
2≤50,∴2b
2+18≤50,∴0<b≤4,又b>3,∴3<b≤4,即6<2b≤8.
∴椭圆C的短轴长的取值范围是(6,8].
分析:(1)先设出P、Q两点的坐标,利用P、Q在x轴上的射影分别为椭圆的左、右焦点,且P、Q两点的连线的斜率为

.即可求椭圆的离心率e的大小;
(2)先求出以PQ为直径的圆的方程,利用圆心到直线的距离等于半径求出b值即可求椭圆C的标准方程;
(3)先利用点M(0,3)在椭圆内部求出b的一个范围,再利用两点间的距离公式以及最远距离不大于

,求出b的另一个范围,两个相综合可得椭圆C的短轴长的取值范围.
点评:本题是对圆与椭圆知识的综合考查.当直线与圆相切时,可以利用圆心到直线的距离等于半径求解,也可以把直线与圆的方程联立让对应方程的判别式为0求解.本题用的是方法一.

 上两点P、Q在x轴上的射影分别为椭圆的左、右焦点,且P、Q两点的连线的斜率为
上两点P、Q在x轴上的射影分别为椭圆的左、右焦点,且P、Q两点的连线的斜率为 .
. ,求椭圆C的短轴长的取值范围.
,求椭圆C的短轴长的取值范围.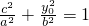 ,
,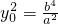 ,
, ,
,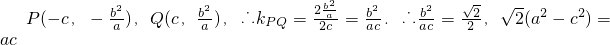 ,
, ,解得
,解得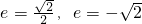 (舍去).
(舍去).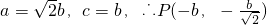 ,
,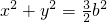 .
.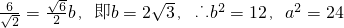 .
.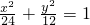 .
. ,故椭圆方程为
,故椭圆方程为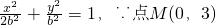 在椭圆内部,
在椭圆内部, ,∴MN2≤50,∴2b2+18≤50,∴0<b≤4,又b>3,∴3<b≤4,即6<2b≤8.
,∴MN2≤50,∴2b2+18≤50,∴0<b≤4,又b>3,∴3<b≤4,即6<2b≤8. .即可求椭圆的离心率e的大小;
.即可求椭圆的离心率e的大小; ,求出b的另一个范围,两个相综合可得椭圆C的短轴长的取值范围.
,求出b的另一个范围,两个相综合可得椭圆C的短轴长的取值范围.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案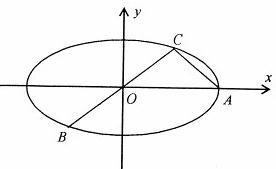 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且 (2010•上虞市二模)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且
(2010•上虞市二模)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且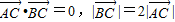 .
.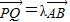 ?请给出证明.
?请给出证明.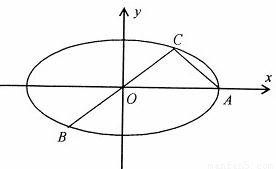
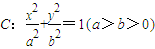 上两点P、Q在x轴上的射影分别为椭圆的左、右焦点,且P、Q两点的连线的斜率为
上两点P、Q在x轴上的射影分别为椭圆的左、右焦点,且P、Q两点的连线的斜率为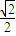 .
.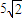 ,求椭圆C的短轴长的取值范围.
,求椭圆C的短轴长的取值范围.