
����Ŀ������������A��B��C����γ���ÿ��γ����������ͺͱ��������ͺţ�ij�µIJ������±�����λ��������
�γ�A | �γ�B | �γ�C | |
������ | 100 | 150 | z |
���� | 300 | 450 | 600 |
�����÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10����
��1����z��ֵ��
��2���÷ֲ�����ķ�����C��γ��г�ȡһ������Ϊ5��������������������һ�����壬������ȡ2������������1�������ͽγ��ĸ��ʣ�
��3������������ķ�����B�������ͽγ��г�ȡ8������������ǵĵ÷����£�9.4��8.6��9.2��9.6��8.7��9.3��9.0��8.2������8���γ��ĵ÷ֿ���һ�����壬������ȡһ�����������������ƽ����֮��ľ���ֵ������0.5�ĸ��ʣ�
���𰸡�
��1���⣺��ó�����¹������γ�n����
������� ![]() =
= ![]() ��
��
��n=2000��
��z=2000����100+300����150��450��600=400��
��2���⣺��������������a�������ͽγ���
�����⣬��a=2��
��˳�ȡ������Ϊ5�������У�
��2�������ͽγ���3�����ͽγ���
��A1��A2��ʾ2�������ͽγ���
��B1��B2��B3��ʾ3�����γ���
��E��ʾ�¼����ڸ���������ȡ2��������������1�������ͽγ�����
������¼��ռ�����Ļ����¼��У�
��A1��A2������A1B1������A1B2����
��A1��B3��������A2��B1������A2��B2����A2��B3����
��B1B2������B1��B3��������B2��B3������10����
�¼�E�����Ļ����¼��У�
��A1A2������A1��B1��������A1��B2������A1��B3����
��A2��B1������A2��B2������A2��B3������7����
�� P��E��= ![]() ��
��
���������Ϊ ![]() ��
��
��3���⣺����ƽ���� ![]() =
= ![]() ��9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2��=9��
��9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2��=9��
��D��ʾ�¼�������������ȡһ����
����������ƽ����֮��ľ��Բ�����0.5����
������¼��ռ�����8�������¼���
�¼�D�����Ļ����¼��У�9.4��8.6��9.2��8.7��9.3��9.0����6����
��P��D��= ![]() �����������Ϊ
�����������Ϊ ![]() ��
��
����������1�������÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10������ÿ�����屻�鵽�ĸ��ʣ��г���ϵʽ���õ�n��ֵ��2��������֪������һ���ŵ���ͣ����鷢���������¼����������������¼���������ͨ���о�������������ݹŵ���͵ĸ��ʹ�ʽ�õ��������3����������������ƽ�������������鷢���������¼������������������¼��������ݹŵ���͵ĸ��ʹ�ʽ�õ������
�����㾫�������÷ֲ��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ���������������������������


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��cos
=��cos ![]() x��sin
x��sin ![]() x����
x���� ![]() =��cos
=��cos ![]() ����sin
����sin ![]() ������x��[��
������x��[�� ![]() ��
�� ![]() ]
]
��1���� ![]()
![]() ��|
��| ![]() +
+ ![]() |��
|��
��2����f��x��= ![]()
![]() ��|
��| ![]() +
+ ![]() |����f��x�������ֵ����Сֵ��
|����f��x�������ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=sinx��ͼ�������еĵ�����ƽ���ƶ� ![]() ����λ���ȣ��ٰ����ø���ĺ������쳤��ԭ����2���������겻�䣩������ͼ��ĺ�������ʽ�ǣ� ��
����λ���ȣ��ٰ����ø���ĺ������쳤��ԭ����2���������겻�䣩������ͼ��ĺ�������ʽ�ǣ� ��
A.y=sin��2x�� ![]() ��
��
B.y=sin��2x+ ![]() ��
��
C.y=sin�� ![]() x��
x�� ![]() ��
��
D.y=sin�� ![]() x��
x�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����
������1��������![]() �ǵ�����������
�ǵ�����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����֤����![]() ʱ������
ʱ������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() +
+ ![]() ����������������ȷ���������� ��
����������������ȷ���������� ��
��f��x����ż������
��f��x����ֵ����[ ![]() ��2]��
��2]��
�۵�x��[0�� ![]() ]ʱ��f��x������������
]ʱ��f��x������������
�ܵ��ҽ���x=2k�С� ![]() ��k��Z��ʱ��f��x��=
��k��Z��ʱ��f��x��= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn�����Sn �� ��Sn+ ![]() an=1��n��N+��
an=1��n��N+��
��1��������{an}��ͨ�ʽ��
��2����bn= ![]() ��1��Sn+1����n��N+������Tn=
��1��Sn+1����n��N+������Tn= ![]() ����Tn ��
����Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD������PAD�DZ߳�Ϊ2���������Σ�������洹ֱ������ABCD�ǡ�ABC=60������Σ�MΪPC���е㣮
���� ��֤��PC��AD��
���� ����PB���Ƿ����һ��Q��ʹ��A��Q��M��D�ĵ㹲�棿�����ڣ�ָ����Q��λ�ò�֤�����������ڣ���˵�����ɣ�
���� ���D��ƽ��PAM�ľ��룮 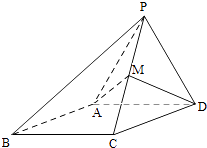
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ԲO��ֱ��AB����Ϊ4����DΪ�߶�AB��һ�㣬�� ![]() ����CΪԲO��һ�㣬��
����CΪԲO��һ�㣬�� ![]() ����P��ԲO����ƽ���ϵ���ͶӰΪ��D��PD=BD��
����P��ԲO����ƽ���ϵ���ͶӰΪ��D��PD=BD�� 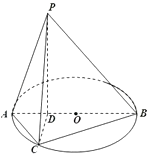
��1����֤��CD��ƽ��PAB��
��2�����D��ƽ��PBC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ���˳���Сʯ����ɳ̲�ϰڳɸ�����״���о���.���磺 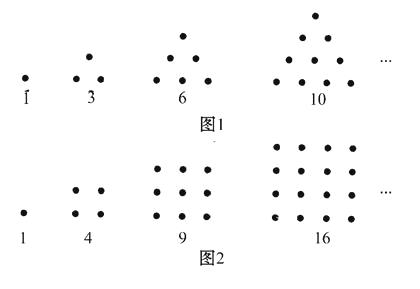
�����о���ͼ1�е�1��3��6��10������������Щ���ܹ���ʾ�������Σ������Ϊ�������������Ƶأ���ͼ2�е�1��4��9��16��������������Ϊ��������.�������м���������������������������( )
A.289
B.1024
C.1225
D.1378
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com