
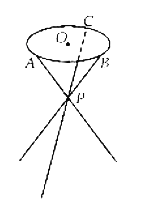
【题目】如图,小凳凳面为圆形,凳脚为三根细钢管.考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点![]() 与凳面圆形的圆心
与凳面圆形的圆心![]() 的连线垂直于凳面和地面,且
的连线垂直于凳面和地面,且![]() 分细钢管上下两段的比值为
分细钢管上下两段的比值为![]() ,三只凳脚与地面所成的角均为
,三只凳脚与地面所成的角均为![]() .若
.若![]() 、
、![]() 、
、![]() 是凳面圆周的三等分点,
是凳面圆周的三等分点,![]() 厘米,求凳子的高度
厘米,求凳子的高度![]() 及三根细钢管的总长度(精确到
及三根细钢管的总长度(精确到![]() ).
).
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()
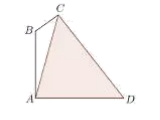
(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在区间
,若在区间![]() 内有且只有一个实数
内有且只有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(1)判断函数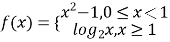 在区间
在区间![]() 内是否具有唯一零点,说明理由:
内是否具有唯一零点,说明理由:
(2)已知向量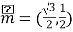 ,
,![]() ,
,![]() ,证明
,证明![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)若函数![]() 在区间
在区间![]() 内具有唯一零点,求实数
内具有唯一零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() 都有
都有![]() 成立(其中
成立(其中![]() 是常数).
是常数).
(1)当![]() 时,求
时,求![]() :
:
(2)当![]() 时,
时,
①若![]() ,求数列
,求数列![]() 的通项公式:
的通项公式:
②设数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“![]() 数列”,如果
数列”,如果![]() ,试问:是否存在数列
,试问:是否存在数列![]() 为“
为“![]() 数列”,使得对任意
数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() ,若存在,求数列
,若存在,求数列![]() 的首项
的首项![]() 的所有取值构成的集合;若不存在.说明理由.
的所有取值构成的集合;若不存在.说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
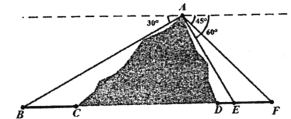
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com