[题目]有这样一个问题:从冬至日起.依次小寒.大寒.立春.雨水.惊蛰.春分.清明.谷雨.立夏.小满.芒种十二个节气日影长减等寸.雨水.惊蛰.春分.清明日影之和为三丈二尺.前七个节气日影之和为七丈三尺五寸.问立夏日影长为( )A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】《周髀算经》有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，雨水、惊蛰、春分、清明日影之和为三丈二尺，前七个节气日影之和为七丈三尺五寸，问立夏日影长为（）

A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸

【答案】D

【解析】

利用等差数列的通项公式以及求和公式列出方程组，求出首项和公差，由此可求得立夏日影长.

从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，雨水、惊蛰、春分、清明日影之和为三丈二尺，前七个节气日影之和为七丈三尺五寸，

设十二节气第个节气的日影长为，则数列为等差数列，设其公差为，前项和为，

则，解得，

，因此，立夏日影长为四尺五寸.

故选：D.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】共享单车又称为小黄车，近年来逐渐走进了人们的生活，也成为减少空气污染，缓解城市交通压力的一种重要手段．为调查某地区居民对共享单车的使用情况，从该地区居民中按年龄用随机抽样的方式随机抽取了人进行问卷调查，得到这人对共享单车的评价得分统计填入茎叶图，如下所示（满分分）：

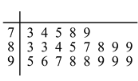
（1）找出居民问卷得分的众数和中位数；

（2）请计算这位居民问卷的平均得分；

（3）若在成绩为分的居民中随机抽取人，求恰有人成绩超过分的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）求曲线在处的切线方程，并证明：.

（2）当时，方程有两个不同的实数根，证明：.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】关于函数有下述四个结论：

①是偶函数；②的最大值为；

③在有个零点；④在区间单调递增.

其中所有正确结论的编号是（）

A.①②B.①③C.②④D.①④

查看答案和解析>>

科目：高中数学 来源： 题型：

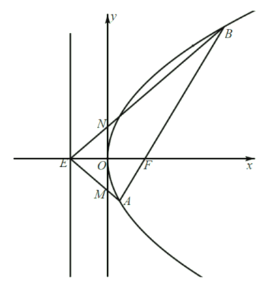
【题目】如图，抛物线的焦点为，是抛物线的准线与轴的交点，直线经过焦点且与抛物线相交于、两点，直线、分别交轴于、两点，记、的面积分别为、.

（1）求证：；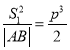

（2）若恒成立，求实数的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛，于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩，将统计情况绘制成如图所示的折线图.根据该折线图，下面结论正确的是（）

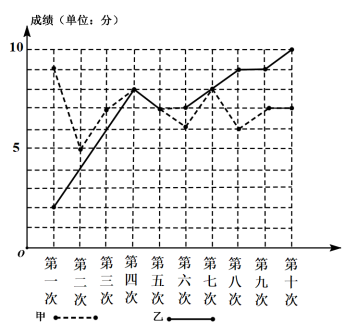
A.甲、乙成绩的中位数均为7

B.乙的成绩的平均分为6.8

C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率

D.甲的成绩的方差小于乙的成绩的方差

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面，底面为直角梯形，分别为的中点.

（1）求证：平面；

（2）若截面与底面所成锐二面角为，求的长度.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对n个不同的实数a1，a2，…，an可得n！个不同的排列，每个排列为一行写成一个n！行的数阵.对第i行ai1，ai2，…，ain，记bi=－ai1+2ai2－3ai3+…+(－1)nnain，i=1，2，3…，n！.例如用1，2，3可得数阵如图，对于此数阵中每一列各数之和都是12，所以bl+b2+…b6=－12+2×12－3×12=－24.那么，在用1，2，3，4，5形成的数阵中，b1+b2+…b120等于（）