B
分析:先设P(x,y) A(-1,0),B(1,0)分别表示出

,

,
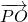
,根据把

,

代入|PA|•|PB|=PO
2整理可得x
2-y
2=

可知点P的轨迹为双曲线,通过与圆的方程联立即可求得它们的交点,得x
2=

,但P(x,y)在圆内,故对P,只能x
2<

,又根据x
2-y
2=

可知x
2>=

,进而可得的x
2范围,设z=

•

=x
2-1+y
2,把x
2-y
2=

代入z,进而可得答案.
解答:设P(x,y) A(-1,0),B(1,0)
则

=(-1-x,-y)

=(1-x,-y)
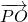
=(-x,-y)
设z=PA•PB=x
2-1+y
2.(1)
又∵|PA|•|PB|=PO
2∴[(1+x)
2+y
2]•[(1-x)
2+y
2]=(x
2+y
2)
2
整理得:x
2-y
2=

(2)
这是P点满足的条件 (其图形为一双曲线)
求它与圆的交点:
即,解方程组:
x
2+y
2=1.(3)
x
2-y
2=

(4)
得x
2=

(5)
(但P(x,y)在圆内,故对P,只能x
2<

又由(2)知x
2>=

,
即

≤x
2<

(6)
由(2)还得:y
2=x
2-

代入(1),得
z=2x
2-

(7)
由((6),(7)知,z的取值范围为
为:[-

,0)
故选B
点评:本题主要考查了等比数列和平面向量的性质.要特别把握好平面向量的运算法则.

 的取值范围为
的取值范围为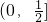
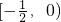
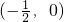
 ,
, ,
,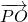 ,根据把
,根据把 ,
, 代入|PA|•|PB|=PO2整理可得x2-y2=
代入|PA|•|PB|=PO2整理可得x2-y2= 可知点P的轨迹为双曲线,通过与圆的方程联立即可求得它们的交点,得x2=
可知点P的轨迹为双曲线,通过与圆的方程联立即可求得它们的交点,得x2= ,但P(x,y)在圆内,故对P,只能x2<
,但P(x,y)在圆内,故对P,只能x2< ,又根据x2-y2=
,又根据x2-y2= 可知x2>=
可知x2>= ,进而可得的x2范围,设z=
,进而可得的x2范围,设z= •
• =x2-1+y2,把x2-y2=
=x2-1+y2,把x2-y2= 代入z,进而可得答案.
代入z,进而可得答案. =(-1-x,-y)
=(-1-x,-y) =(1-x,-y)
=(1-x,-y)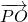 =(-x,-y)
=(-x,-y) (2)
(2) (4)
(4) (5)
(5)
 ,
, ≤x2<
≤x2< (6)
(6)
 (7)
(7) ,0)
,0)
