
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| 3 |
| OM |
| ON |
| x |
| a |
| y |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
| y0 |
| x0+a |
| y0 |
| x0-a |
| y02 |
| x02-a2 |
| 1 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| (kx+m)2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a |
| y |
| b |
| 1 | ||||||
|
| 1 |
| a2 |
| 1 |
| b2 |
| y0 |
| x0+a |
| y0 |
| x0-a |
| y02 |
| x02-a2 |
| 1 |
| 3 |
| x02 |
| a2 |
| 3y02 |
| a2 |
| x02 |
| a2 |
| y02 |
| b2 |
| 1 |
| 3 |
| 1 |
| a2 |
| 1 |
| b2 |
| 4 |
| 3 |
| x2 |
| 4 |
| 3y2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| (kx+m)2 |
| b2 |
| a2m2-a2b2 |
| b2+a2k2 |
| a2k2m2-a2b2k2 |
| b2+a2k2 |
| 2a2km |
| b2+a2k2 |
| b2m2-a2b2k2 |
| b2+a2k2 |
| OM |
| ON |
| 1 |
| a2 |
| 1 |
| b2 |
| |m| | ||
|
| x2 |
| a2 |
| y2 |
| b2 |
1-
|
1-
|
| a2b2 |
| a2+b2 |
| 1 |
| a2 |
| 1 |
| b2 |
| a2b2 |
| a2+b2 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
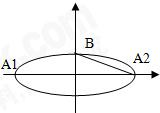
(09年海淀区期末文)(14分)
已知椭圆![]() A1、A2、B是椭圆的顶点(如图),直线
A1、A2、B是椭圆的顶点(如图),直线![]() 与椭圆交于异于椭圆顶点的P、Q两点,且
与椭圆交于异于椭圆顶点的P、Q两点,且![]() //A2B。若此椭圆的离心率为
//A2B。若此椭圆的离心率为![]()
(I)求此椭圆的方程;
(II)设直线A1P和直线BQ的倾斜角分别为![]() 是否为定值?若是,求出此定值;若不是,请说明理由。
是否为定值?若是,求出此定值;若不是,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市海淀区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟预测文科数学试卷(解析版) 题型:解答题
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
【解析】本试题主要考查了统计和概率的综合运用。
第一问工厂总数为18+27+18=63,样本容量与总体中的个体数比为7/63=1/9…3分
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。
第二问设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。
这7个工厂中随机的抽取2个,全部的可能结果有1/2*7*6=32种。
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。
所以所求的概率为p=11/21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com