
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,请说明理由.
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题4练习卷(解析版) 题型:填空题
抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 87 | 91 | 90 | 89 | 93 |
乙 | 89 | 90 | 91 | 88 | 92 |
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题1练习卷(解析版) 题型:填空题
设函数f(x)=x(ex+ae-x)(x∈R)是偶函数,则实数a的值为______________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积大于20 cm2的概率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:解答题
设椭圆M: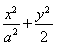 =1(a>
=1(a>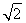 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x=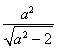 与x轴交于点A,若
与x轴交于点A,若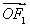 =2
=2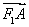 (其中O为坐标原点).
(其中O为坐标原点).
(1)求椭圆M的方程;
(2)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E,F为直径的两个端点),求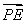 ·
·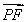 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
设F是双曲线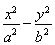 =1的右焦点,双曲线两条渐近线分别为l1,l2,过F作直线l1的垂线,分别交l1,l2于A、B两点.若OA,AB,OB成等差数列,且向量
=1的右焦点,双曲线两条渐近线分别为l1,l2,过F作直线l1的垂线,分别交l1,l2于A、B两点.若OA,AB,OB成等差数列,且向量 与
与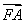 同向,则双曲线离心率e的大小为________.
同向,则双曲线离心率e的大小为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
已知圆(x+1)2+(y-1)2=1上一点P到直线3x-4y-3=0距离为d,则d的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an} 的前n项和Sn=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
已知定义在R上的函数f(x)的图象关于原点对称,其最小正周期为4,且x∈(0,2)时,f(x)=log2(1+3x),则f(2 015)=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com