
分析 (1)根据已知向量加法的三角形法则,及正方体的几何特征,可将向量$\overrightarrow{OD′}$和$\overrightarrow{OM}$用基底向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示;
(2)根据与$\overrightarrow{a}$同向的单位的向量表示为:$\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$,结合$\overrightarrow{OI}$,$\overrightarrow{OJ}$,$\overrightarrow{OK}$分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$方向上的单位向量,可得答案.
解答 解:(1)由下图所示:正方体OADB-CA′D′B′中,点E是AB与OD的交点,M是OD′与CE的交点,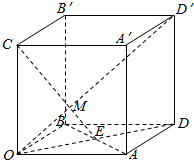
则$\overrightarrow{OD′}$=$\overrightarrow{OA}+\overrightarrow{AD}+\overrightarrow{DD′}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$;
$\overrightarrow{OM}$=$\frac{1}{3}$$\overrightarrow{OD′}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$;
(2)∵$\overrightarrow{OI}$,$\overrightarrow{OJ}$,$\overrightarrow{OK}$分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$方向上的单位向量,
∴$\overrightarrow{OA}$=|$\overrightarrow{OA}$|$\overrightarrow{OI}$,$\overrightarrow{OB}$=|$\overrightarrow{OB}$|$\overrightarrow{OJ}$,$\overrightarrow{OC}$=|$\overrightarrow{OC}$|$\overrightarrow{OK}$.
点评 本题考查的知识点是空间向量加法的三角形法则,空间向量的基本定理,难度不大,属于基础题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $10\sqrt{2}$ | C. | $10\sqrt{3}$ | D. | $\frac{{10\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com