【答案】
分析:(Ⅰ)设出双曲线的标准方程,然后结合椭圆的顶点与焦点易得双曲线的焦点与顶点,即求得双曲线的c与a,再由a
2+b
2=c
2求得b
2,则双曲线方程解决;
(Ⅱ)把直线方程分别与椭圆方程、双曲线方程联立,不妨消y得x的方程,则它们均为一元二次方程且判别式大于零,由此得出k的取值范围;再结合一元二次方程根与系数的关系用k的代数式表示出x
A+x
B,x
Ax
B,进而把
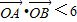
转化为k的不等式,求出k的又一取值范围,最后求k的交集即可.
解答:解:(Ⅰ)设双曲线C
2的方程为
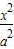
-

=1,则a
2=4-1=3,再由a
2+b
2=c
2得b
2=1.
故C
2的方程为
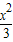
-y
2=1.
(II)将y=kx+
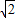
代入

+y
2=1得(1+4k
2)x
2+8
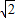
kx+4=0
由直线l与椭圆C
1恒有两个不同的交点得△1=
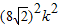
-16(1+4k
2)=16(4k
2-1)>0,
即k
2>

①
将y=kx+
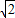
代入

-y
2=1得(1-3k
2)x
2-6
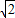
kx-9=0.
由直线l与双曲线C
2恒有两个不同的交点A,B得
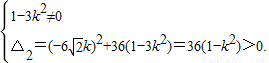
即k
2≠

且k
2<1.②
设A(x
A,y
A)B(x
B,y
B),则x
A+x
B=
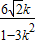
,x
A•x
B=

.
由
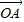
•
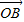
<6得x
Ax
B+y
Ay
B<6,
而x
Ax
B+y
Ay
B=x
Ax
B+(kx
A+
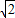
)(kx
B+
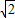
)
=(k
2+1)x
Ax
B+

(x
A+x
B)+2
=(k
2+1)•
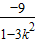
+
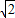
k•
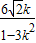
+2
=

.
于是

<6,即
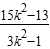
>0.
解此不等式得k
2>

或k
2<

.③
由①、②、③得

<k
2<或
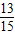
<k
2<1.
故k的取值范围为(-1,-
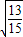
)∪(-
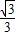
,-

)∪(

,
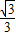
)∪(
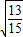
,1).
点评:本题考查双曲线的标准方程以及直线和圆锥曲线的位置关系,综合性强,字母运算能力是一大考验.

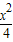 +y2=1,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
+y2=1,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.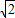 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足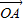 •
•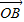 <6(其中O为原点),求k的取值范围.
<6(其中O为原点),求k的取值范围.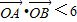 转化为k的不等式,求出k的又一取值范围,最后求k的交集即可.
转化为k的不等式,求出k的又一取值范围,最后求k的交集即可.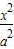 -
- =1,则a2=4-1=3,再由a2+b2=c2得b2=1.
=1,则a2=4-1=3,再由a2+b2=c2得b2=1.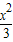 -y2=1.
-y2=1.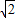 代入
代入 +y2=1得(1+4k2)x2+8
+y2=1得(1+4k2)x2+8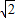 kx+4=0
kx+4=0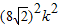 -16(1+4k2)=16(4k2-1)>0,
-16(1+4k2)=16(4k2-1)>0, ①
①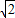 代入
代入 -y2=1得(1-3k2)x2-6
-y2=1得(1-3k2)x2-6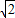 kx-9=0.
kx-9=0.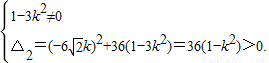
 且k2<1.②
且k2<1.②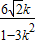 ,xA•xB=
,xA•xB= .
.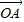 •
•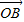 <6得xAxB+yAyB<6,
<6得xAxB+yAyB<6,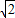 )(kxB+
)(kxB+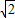 )
) (xA+xB)+2
(xA+xB)+2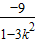 +
+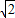 k•
k•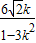 +2
+2 .
. <6,即
<6,即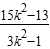 >0.
>0. 或k2<
或k2< .③
.③ <k2<或
<k2<或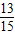 <k2<1.
<k2<1.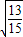 )∪(-
)∪(-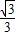 ,-
,- )∪(
)∪( ,
,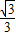 )∪(
)∪(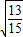 ,1).
,1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案