
| 赞同 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
| P(K2≥K) | 0.25 | 0.15 | 0.10 |
| k | 1.323 | 2.072 | 2.706 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 25×(5×3-6×11)2 |
| 16×9×11×14 |
| ||||||||
|
| ||||
|
| 25×(5×3-6×11)2 |
| 16×9×11×14 |
| ||||||||
|
| 11 |
| 16 |
| ||||
|
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 21 |
| 15 |
| 28 |
| 3 |
| 14 |
| 1 |
| 84 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012届度河北省唐山市高三年级第一次模拟考试数学试卷 题型:解答题
某媒体对“男女同龄退佈”这一公众关注的问题进行了民意调査,右表是在某单位得到的数据(人数):
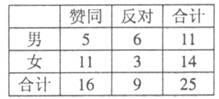
(I )能否有90%以上的把握认为对这一问题的看法与性别有关?
(II)进一步调查:
(i )从赞同“男女同龄退休” 16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ii )从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和均值.
附:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com