
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组![]() 制作了频率分布直方图,
制作了频率分布直方图,
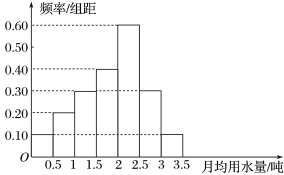
(Ⅰ)用该样本估计总体:
(1)估计该市居民月均用水量的平均数;
(2)如果希望86%的居民每月的用水量不超出标准,则月均用水量a的最低标准定为多少吨?
(Ⅱ)在该样本中月均用水量少于1吨的居民中随机抽取两人,其中两人月均用水量都不低于0.5吨的概率是多少?
【答案】(Ⅰ)(1)1.875;(2)2.7吨;(Ⅱ)![]() .
.
【解析】
(Ⅰ)(1)根据平均数![]() 小矩形的面积乘以小矩形底边中点横坐标之和,代入数据即可求解;(2)由图可得
小矩形的面积乘以小矩形底边中点横坐标之和,代入数据即可求解;(2)由图可得![]() ,解方程即可.
,解方程即可.
(Ⅱ)由直方图可知月均用水量在![]() 的人数为
的人数为![]() ,记为:
,记为:![]() ;月均用水量在
;月均用水量在![]() 的人数为
的人数为![]() ,记为:A,B,C,D ,列举出抽取两人所有可能的情况,找出月均用水量都在
,记为:A,B,C,D ,列举出抽取两人所有可能的情况,找出月均用水量都在![]() 的情况,利用古典概型的概率计算公式即可求解.
的情况,利用古典概型的概率计算公式即可求解.
(Ⅰ)(1)月均用水量
![]()
![]()
(2)由直方图易知:![]() ,由
,由![]() 吨
吨
故月均用水量a的标准定为2.7吨.
(Ⅱ)由直方图可知:月均用水量在![]() 的人数为:
的人数为:![]() 人,
人,
记为:![]()
月均用水量在![]() 的人数为:
的人数为:![]() 人,
人,
记为:A,B,C,D
从此6人中随机抽取两人所有可能的情况有:![]() 共15种,
共15种,
其中月均用水量都在![]() 的情况有:
的情况有:![]() 共6种,
共6种,
故两人月均用水量都不低于0.5吨的概率:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若直线![]() 且曲线
且曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,求a的取值范围;
在B处的切线相互平行,求a的取值范围;
(Ⅱ)设![]() 在其定义域内有两个不同的极值点
在其定义域内有两个不同的极值点![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥PABC的各顶点都在同一球面上,![]() 底面ABC,若
底面ABC,若![]() ,
,![]() ,且
,且![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.![]() 是钝角三角形B.此球的表面积等于
是钝角三角形B.此球的表面积等于![]()
C.![]() 平面PACD.三棱锥APBC的体积为
平面PACD.三棱锥APBC的体积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
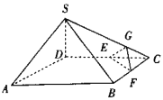
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个好朋友小聪和小明,在同一天小聪从深圳到黄石,中午到武汉站的时间为13:30,然后再乘坐城际铁路到黄石,中间有1小时在武汉站候车室休息.小明从沌口开发区坐出租车到武汉站,小明到达武汉站的时间为14:00~15:00之间任一时刻到达,然后乘坐发车时间为15:30的高铁到北京,那么两个好朋友能够在武汉站会面的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com