
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 的中点.
的中点.

(1)证明:平面![]() ∥平面
∥平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,利用线面平行的判定定理和面面平行的判定定理即可证明;
,利用线面平行的判定定理和面面平行的判定定理即可证明;
(2)由线面垂直的性质可得,![]() ,故
,故![]() 、
、![]() 、
、![]() 两两互相垂直,
两两互相垂直,
以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,设平面
轴,建立空间直角坐标系,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量法,则空间向量
,利用空间向量法,则空间向量![]() 所成角的余弦值的绝对值即为所求.
所成角的余弦值的绝对值即为所求.
(1)证明:连接![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,如图,
,如图,
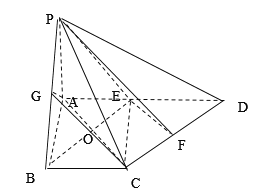
因为![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,
所以四边形![]() 为矩形,
为矩形,
所以![]() 为
为![]() 的中点,又因为
的中点,又因为![]() 为
为![]() 的中点,
的中点,
所以![]() 为
为![]() 的中位线,即
的中位线,即![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() ∥平面
∥平面![]() .
.
(2)因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() 、
、![]() 、
、![]() 两两互相垂直,
两两互相垂直,
以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,
轴,
建立空间直角坐标系,如图所示:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
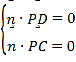 ,所以
,所以![]() ,
,
令![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为利于分层教学,某学校根据学生的情况分成了![]() ,
,![]() ,
,![]() 三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 145 | 83 | 95 | 72 | 110 |
![]() ,
,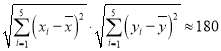 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 93 | 90 | 76 | 101 |
![]() ,
,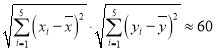 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 92 | 101 | 100 | 112 |
![]() ,
,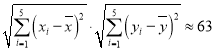 ;
;
(1)经计算已知![]() ,
,![]() 的相关系数分别为
的相关系数分别为![]() ,
,![]() ,请计算出
,请计算出![]() 学生的
学生的![]() 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,![]() 越大认为成绩越稳定);
越大认为成绩越稳定);
(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归方程为![]() ,利用线性回归方程预测该生第九次的成绩.
,利用线性回归方程预测该生第九次的成绩.
参考公式:(1)样本![]() 的相关系数
的相关系数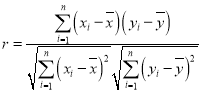 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为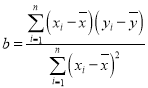 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
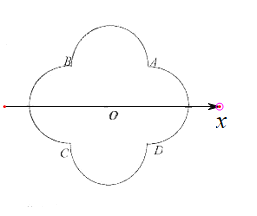
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,如图所示,在宝塔形数表中位于第![]() 行,第
行,第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ( )
( )
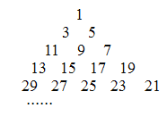
A.64B.65C.71D.72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
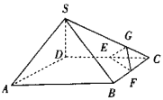
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是我国古代的天文学和数学著作.其中有一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).二十四个节气及晷长变化如图所示,若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至后的那个节气(小暑)晷长为( )
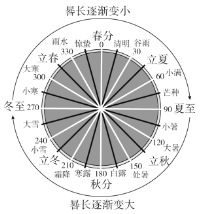
A.五寸B.二尺五寸C.三尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的标准长度为![]() ,只要误差的绝对值不超过
,只要误差的绝对值不超过![]() 就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
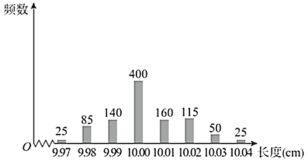
(1)估计该批次产品长度误差绝对值的数学期望;
(2)如果视该批次产品样本的频率为总体的概率,要求从工厂生产的产品中随机抽取2件,假设其中至少有1件是标准长度产品的概率不小于0.8时,该设备符合生产要求.现有设备是否符合此要求?若不符合此要求,求出符合要求时,生产一件产品为标准长度的概率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体 ABCD 中,P,Q分别是棱 AB,CD的中点,E,F分别是直线AB,CD上的动点,M 是EF 的中点,则能使点 M 的轨迹是圆的条件是( )
A. PE+QF=2B. PEQF=2
C. PE=2QFD. PE2+QF2=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com