
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x、y轴分别交于点
与x、y轴分别交于点![]() 、
、![]() ,记以点
,记以点![]() 为圆心,半径为r的圆与三角形
为圆心,半径为r的圆与三角形![]() 的边的交点个数为M.对于下列说法:①当
的边的交点个数为M.对于下列说法:①当![]() 时,若
时,若![]() ,则
,则![]() ;②当
;②当![]() 时,若
时,若![]() ,则
,则![]() ;③当
;③当![]() 时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是梯形,AB//CD,DA⊥AB,BC⊥SC,SA=AD=3,AB=6,点E在棱SD上,且VS-ACE=2VE-ACD。

(1)求证:BC⊥平面SAC;
(2)求二面角S-AE-C的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
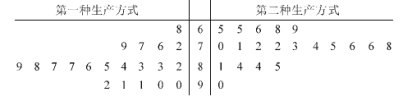
(1)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: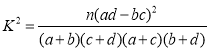
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
(1)证明函数![]() 是“正函数”;
是“正函数”;
(2)如果函数![]() 不是“正函数”,求正数a的取值范围.
不是“正函数”,求正数a的取值范围.
(3)如果函数 是“正函数”,求正数a的取值范围.
是“正函数”,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
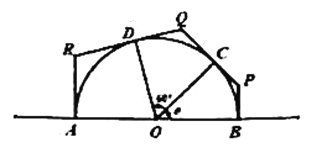
【题目】为美化城市环境,相关部门需对一半圆形中心广场进行改造出新,为保障市民安全,施工队对广场进行围挡施工.如图,围挡经过直径的两端点A,B及圆周上两点C,D围成一个多边形ABPQR,其中AR,RQ,QP,PB分别与半圆相切于点A,D,C,B.已知该半圆半径OA长30米,∠COD为60°,设∠BOC为![]() .
.
(1)求围挡内部四边形OCQD的面积;
(2)为减少对市民出行的影响,围挡部分面积要尽可能小.求该围挡内部多边形ABPQR面积的最小值?并写出此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有8名马拉松比赛志愿者,其中志愿者![]() ,
,![]() ,
,![]() 通晓日语,
通晓日语,![]() ,
,![]() ,
,![]() 通晓俄语,
通晓俄语,![]() ,
,![]() 通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
![]() 列出基本事件;
列出基本事件;
![]() 求
求![]() 被选中的概率;
被选中的概率;
![]() 求
求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1-![]() (a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(1)求a的值;
(2)证明:函数f(x)在定义域(-∞,+∞)内是增函数;
(3)当x∈(0,1]时,tf(x)≥2x-2恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com