练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设函数f（x）在点x0附近有定义，且有f（x0+△x）-f（x0）=a△x+b（△x）2，其中a，b为常数，则（　　）
    A．f'（x）=aB．f'（x）=bC．f'（x0）=aD．f'（x0）=b

    分析 根据导数的定义即可求出答案．

    解答 解：∵f（x0+△x）-f（x0）=a△x+b（△x）2，
    ∴$\frac{f（{x}_{0}+△x）-f（{x}_{0}）}{△x}$=a+b△x，
    ∴f′（x0）=$\underset{lim}{△x→0}$$\frac{f（{x}_{0}+△x）-f（{x}_{0}）}{△x}$=$\underset{lim}{△x→0}$（a+b△x）=a，
    故选：C

    点评 本题考查导数的计算，关键是熟悉导数的定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知函数f（x）=$\left\{\begin{array}{l}{|lnx|，0＜x≤{e}^{3}}\\{-x+{e}^{3}+3，x＞{e}^{3}}\end{array}\right.$，存在x1＜x2＜x3，f（x1）=f（x2）=f（x3），则$\frac{f（{x}_{3}）}{{x}_{2}}$的最大值为$\frac{1}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．直线$\left\{\begin{array}{l}x=1-\frac{1}{2}t\\ y=-3\sqrt{3}+\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数）和圆x2+y2=16交于A，B两点，则AB的中点坐标为（　　）
    A．（3，-3）B．$（-\sqrt{3}，3）$C．$（\sqrt{3}，-3）$D．（-$\frac{3}{2}$，-$\frac{\sqrt{3}}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=2cos（$\frac{π}{2}$-ωx）+2sin（$\frac{π}{3}$-ωx）（ω＞0，x∈R），若f$（\frac{π}{6}）$+f$（\frac{π}{2}）$=0，且f（x）在区间$（\frac{π}{6}，\frac{π}{2}）$上递减．
    （1）求f（0）的值；     
    （2）求ω；
    （3）解不等式f（x）≥1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知两圆相交于A（-1，3），B（-6，m）两点，且这两圆的圆心均在直线x-y+c=0上，则m+2c的值为（　　）
    A．-1B．26C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

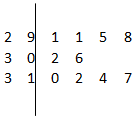    14．如图是根据我省的统计年鉴中的资料做成的2007年至2016年我省城镇居民百户家庭人口数的茎叶图．图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字，右边的数字表示城镇居民百户家庭人口数的个位数字．从图中可以得到2007年至2016年我省城镇居民百户家庭人口数的平均数为303.6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．（2x-3）4=a0+a1x+a2x2+a3x3+a4x4，求
    （1）a1+a2+a3+a4．
    （2）（a0+a2+a4）2-（a1+a3）2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=|x-a|+|x-3a|．
    （1）若f（x）的最小值为2，求a的值；
    （2）若对?x∈R，?a∈[-1，1]，使得不等式m2-|m|-f（x）＜0成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知实数x，y满足不等式组$\left\{\begin{array}{l}x-3y+5≥0\\ 2x+y-4≤0\\ y+2≥0\end{array}\right.$则z=x+y的最小值为-13．

    查看答案和解析>>

    同步练习册答案