
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点 .
.
(1)求椭圆的方程;
(2)设不过原点![]() 的直线
的直线![]() 与该椭圆交于
与该椭圆交于![]() 两点,满足直线
两点,满足直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设出椭圆的方程,将已知点代入椭圆的方程及利用椭圆的离心率公式得到关于椭圆的三个参数的等式,解方程组求出a,b,c的值,代入椭圆方程即可.
(2)设出直线的方程,将直线方程与椭圆方程联立,消去x得到关于y的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线OP,PQ,OQ的斜率用坐标表示,据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出k的值,利用判别式大于0得到m的范围,将△OPQ面积用m表示,求出面积的范围.
试题解析:
(1)根据题意可设椭圆方程为![]() ,则
,则
则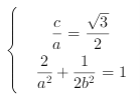 故
故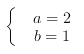 ,所以,椭圆方程为
,所以,椭圆方程为![]() .
.
(2)根据题意可以知道,直线l的斜率存在且不为0,
故可设直线l的方程为![]() ,
,![]() ,
,![]() ,
,
由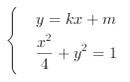 消去y得
消去y得
![]() ,
,
则![]() ,
,
且![]() ,
,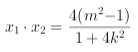 .
.
故![]() .
.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以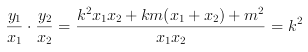 ,
,
即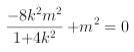 ,又
,又![]() ,所以
,所以![]() ,即
,即![]() .
.
因为直线OP,OQ的斜率存在,且![]() ,得
,得
![]() 且
且![]() .设d为点O到直线l的距离,
.设d为点O到直线l的距离,
则![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在钝角△ABC中,∠A为钝角,令![]() ,若
,若![]() .现给出下面结论:
.现给出下面结论:
①当![]() 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;
;
③若点D在△ABC内部(不含边界),则![]() 的取值范围是
的取值范围是![]() ;
;
④若点D在线段BC上(不在端点),则![]()
⑤若![]() ,其中点E在直线BC上,则当
,其中点E在直线BC上,则当![]() 时,
时,![]() .
.
其中正确的有(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“已知直角三角形两直角边长分别为5步和12步,问其内接正方形边长为多少步?”现若向此三角形内投豆子,则落在其内接正方形内的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“六一”联欢会上设有一个抽奖游戏.抽奖箱中共有12张纸条,分一等奖、二等奖、三等奖、无奖四种.从中任取一张,不中奖的概率为![]() ,中二等奖或三等奖的概率是
,中二等奖或三等奖的概率是![]() .
.
(Ⅰ)求任取一张,中一等奖的概率;
(Ⅱ)若中一等奖或二等奖的概率是![]() ,求任取一张,中三等奖的概率.
,求任取一张,中三等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的高AM所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0与BC相交于点P,若点B的坐标为(1,2).
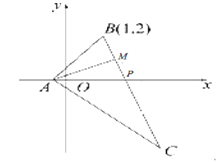
(1)分别求AB和BC所在直线的方程;
(2)求P点坐标和AC所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
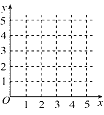
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() =bx+a,
=bx+a,
(3)试预测加工20个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,我校举行传统文化知识竞赛.其中两位选手在个人追逐赛中的比赛得分如茎叶图所示,则下列说法正确的是( )
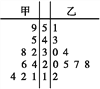
A. 甲的平均数大于乙的平均数
B. 甲的中位数大于乙的中位数
C. 甲的方差大于乙的方差
D. 甲的平均数等于乙的中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com