
【题目】(2016·威海模拟)三人参加某娱乐闯关节目,假设甲闯关成功的概率是![]() ,乙、丙两人同时闯关成功的概率是
,乙、丙两人同时闯关成功的概率是![]() ,甲、丙两人同时闯关失败的概率是
,甲、丙两人同时闯关失败的概率是![]() ,且三人各自能否闯关成功相互独立.
,且三人各自能否闯关成功相互独立.
(1)求乙、丙两人各自闯关成功的概率;
(2)设ξ表示三人中最终闯关成功的人数,求ξ的分布列和均值.
【答案】(1)乙、丙各自闯关成功的概率分别为![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)设甲,乙,丙各自闯关成功的事件分别为A1,A2,A3,它们相互独立,由独立事件的概率公式可列出方程组,从而解得乙、丙的概率;(2)ξ的取值可分别为0,1,2,3,分别计算概率可得分布列,注意各个事件的组成,如事件(![]() )=
)=![]() ,由均值公式可得均值.
,由均值公式可得均值.
试题解析:
(1)记甲,乙,丙各自闯关成功的事件分别为A1,A2,A3,
由已知A1,A2,A3相互独立,且满足
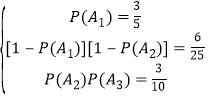
解得![]() .
.
所以乙、丙各自闯关成功的概率分别为![]() ,
,![]() .
.
(2)ξ的可能取值为0,1,2,3.
P(ξ=0)=![]() ,
,
P(ξ=1)=![]() ,
,
P(ξ=2)=![]() ,
,
P(ξ=3)=![]() .
.
所以随机变量ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以随机变量ξ的均值E(ξ)=![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() (其中第一项是
(其中第一项是![]() ,接下来的
,接下来的![]() 项是
项是![]() ,再接下来的
,再接下来的![]() 项是
项是![]() ,依此类推)的前
,依此类推)的前![]() 项和为
项和为![]() ,下列判断:
,下列判断:
①![]() 是
是![]() 的第
的第![]() 项;②存在常数
项;②存在常数![]() ,使得
,使得![]() 恒成立;③
恒成立;③![]() ;④满足不等式
;④满足不等式![]() 的正整数
的正整数![]() 的最小值是
的最小值是![]() .
.
其中正确的序号是( )
A.①③B.①④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面α所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为V1,V2,被平行于这两个平面的任意平面截得的两个截面面积分别为S1,S2,则( )
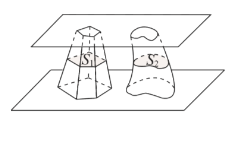
A.如果S1,S2总相等,则V1=V2
B.如果S1=S2总相等,则V1与V2不一定相等
C.如果V1=V2 ,则S1,S2总相等
D.存在这样一个平面α使S1=S2相等,则V1=V2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ,求随机变量ξ的分布列和均值E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,垂足为N , AE⊥PB,垂足为E .
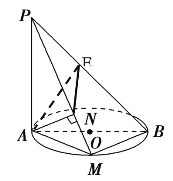
(1)求证:平面PAM⊥平面PBM.
(2)求证:![]() 是二面角A-PB-M的平面角.
是二面角A-PB-M的平面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润![]() 与投资金额x的函数关系为
与投资金额x的函数关系为![]() ,B产品的利润
,B产品的利润![]() 与投资金额x的函数关系为
与投资金额x的函数关系为![]() .(利润与投资金额单位:万元)
.(利润与投资金额单位:万元)
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出x的取值范围.
(2)怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com