
【题目】某气象站观测点记录的连续4天里, ![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位
(单位![]() )的情况如下表1:
)的情况如下表1:
![]()
哈尔滨市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
![]()
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式: ![]() ,其中
,其中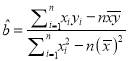 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于200时,洗车店平均每天亏损约2000元;当
不高于200时,洗车店平均每天亏损约2000元;当![]() 在
在![]() 时,洗车店平均每天收入约4000元;当
时,洗车店平均每天收入约4000元;当![]() 大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆![]() 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=y+1上一定点A(﹣1,0)和两动点P,Q,当PA⊥PQ时,点Q的横坐标的取值范围是( )
A.(﹣∞,﹣3]
B.[1,+∞)
C.[﹣3,1]
D.(﹣∞,﹣3]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.
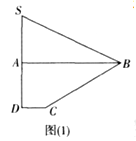
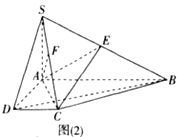
(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表:
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | ﹣2 |
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的二面角的正弦值及四棱锥
所成的二面角的正弦值及四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:
| 1 | 2 | 3 | 4 |
| 12 | 28 | 42 | 56 |

(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:  ,
, ![]() ,
, ![]() .
.
参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com