【题目】已知椭圆C： 
(a>b>0)的一个顶点为A(2,0)，离心率为
.直线y＝k(x－1)与椭圆C交于不同的两点M，N.
(1)求椭圆C的方程；
(2)当△AMN的面积为
时，求k的值．
科目：高中数学 来源： 题型：
【题目】对于下列命题： ①在△ABC中，若sin2A=sin2B，则△ABC为等腰三角形；
②已知a，b，c是△ABC的三边长，若a=2，b=5， 
，则△ABC有两组解；
③设 
， 
， 
，则a＞b＞c；
④将函数 
图象向左平移 
个单位，得到函数 
图象．
其中正确命题的序号是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以原点为圆心，半径为
的圆
与直线
相切.
（1）直线
过点
且截圆所得弦长为
求直线 的方程；
（2）设圆与
轴的正半轴的交点为
，过点作两条斜率分别为
的直线交圆于
两点，且
，证明：直线
恒过一个定点，并求出该定点坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2018河北保定市上学期期末调研】已知点
到点
的距离比到
轴的距离大1．
（I）求点
的轨迹
的方程；
（II）设直线
： 
，交轨迹
于
、
两点， 
为坐标原点，试在轨迹
的
部分上求一点
，使得
的面积最大，并求其最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生，按其数学成绩（均为整数）分成六组
， 
，…， 
后得到如下部分频率分布直方图，观察图中的信息，回答下列问题：
（1）补全频率分布直方图；
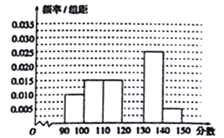
（2）估计本次考试的数学平均成绩（同一组中的数据用该组区间的中点值作代表）；
（3）用分层抽样的方法在分数段为
的学生成绩中抽取一个容量为6的样本，再从这6个样本中任取2人成绩，求至多有1人成绩在分数段
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】张明与张华两人做游戏,下列游戏中不公平的是( )
①抛掷一枚骰子,向上的点数为奇数则张明获胜,向上的点数为偶数则张华获胜;
②同时抛掷两枚硬币,恰有一枚正面向上则张明获胜,两枚都正面向上则张华获胜;
③从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则张明获胜,扑克牌是黑色的则张华获胜;
④张明、张华两人各写一个数字6或8,如果两人写的数字相同张明获胜,否则张华获胜.
A. ①② B. ② C. ②③④ D. ①②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两人玩猜数字游戏，先由甲心中任想一个数字记为
，再由乙猜甲刚才想的数字，把乙猜的数字记为
，且
、
.若
，则称甲乙“心有灵犀”.现任意找两人玩这个游戏，则二人“心有灵犀”的概率为__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
