
【题目】已知数列![]() 满足:
满足: ![]() ,且
,且![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若
项和,若![]() 对任意
对任意![]() 都成立.试求
都成立.试求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题
(1)利用题中的递推关系计算可得后项与前项的比值为定值![]() ,计算首项为
,计算首项为![]() 即可证得数列为等比数列;
即可证得数列为等比数列;
(2)原问题转化为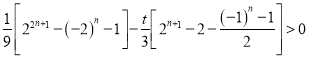 对任意的
对任意的![]() 都成立,分类讨论可得:实数
都成立,分类讨论可得:实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以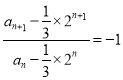 ,
,
又![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)由(Ⅰ)得,![]() ,即
,即![]() ,
,
则![]()
![]()
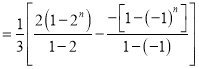
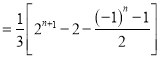 .
.
又![]()
![]() ,
,
要使![]() 对任意的
对任意的![]() 都成立,
都成立,
即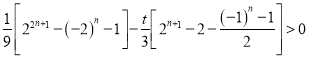 (*)对任意的
(*)对任意的![]() 都成立.
都成立.
①当![]() 为正奇数时,由(*)得,
为正奇数时,由(*)得,![]() ,
,
即![]() ,
,
因为![]() ,
,
所以![]() 对任意的正奇数
对任意的正奇数![]() 都成立,
都成立,
当且仅当![]() 时,
时,![]() 有最小值1,
有最小值1,
所以![]() .
.
②当![]() 为正偶数时,由(*)得,
为正偶数时,由(*)得,
![]() ,
,
即![]() ,
,
因为![]() ,
,
所以![]() 对任意的正偶数
对任意的正偶数![]() 都成立.
都成立.
当且仅当![]() 时,
时,![]() 有最小值
有最小值![]() ,所以
,所以![]() .
.
综上所述,存在实数![]() ,使得
,使得![]() 对任意的
对任意的![]() 都成立,
都成立,
故实数![]() 的取值范围是
的取值范围是![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量![]() ,并根据抽检数据绘制了如下图所示的频率分布直方图.
,并根据抽检数据绘制了如下图所示的频率分布直方图.
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)假设某企业每天由重金属污染造成的经济损失![]() (单位:元)与单位体积河水中重金属含量
(单位:元)与单位体积河水中重金属含量![]()
的关系式为 ,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.
,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 、
、![]() 之间),且
之间),且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() .
.
(1)若直线![]() 不经过第四象限,求
不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,
,![]() 为坐标原点,设
为坐标原点,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列 ![]() 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列;
其中真命题是( )
A.p1 , p2
B.p3 , p4
C.p2 , p3
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=![]() ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;
(2)若圆C1与圆C2相内切,求圆C2的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com