
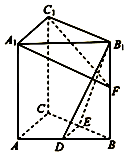
 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.分析 (Ⅰ)由${V}_{B-DE{B}_{1}}$=${V}_{{B}_{1}-BDE}$,能求出三棱锥B-DEB1的体积.
(Ⅱ)推导出AA1⊥A1C1,A1C1⊥A1B1,从而A1C1⊥平面ABB1A1,进而A1C1⊥B1D,再由B1D⊥A1F,能证明平面B1DE⊥平面A1C1F.
解答 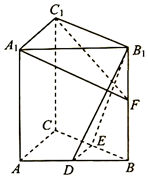 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)∵D,E分别为AB,BC的中点,
∴DE∥AC,$DE=\frac{1}{2}AC=\frac{3}{2}$,$BD=\frac{1}{2}AB=2$.(2分)
∵A1C1⊥A1B1,∴AC⊥AB,DE⊥DB.(3分)
∴${S_{△BDE}}=\frac{1}{2}BD•DE=\frac{1}{2}×2×\frac{3}{2}=\frac{3}{2}$.(4分)
∵ABC-A1B1C1是直三棱柱,∴B1B⊥平面ABC,BB1=AA1=4,
∴${V}_{{B}_{1}-BDE}$=$\frac{1}{3}×B{B}_{1}$×S△BDE=$\frac{1}{3}×4×\frac{3}{2}$=2,(5分)
∵${V}_{B-DE{B}_{1}}$=${V}_{{B}_{1}-BDE}$,∴三棱锥B-DEB1的体积为2.(6分)
证明:(Ⅱ)在直三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C,
∵A1C1?平面A1B1C1,∴AA1⊥A1C1.(7分)
又∵A1C1⊥A1B1,AA1?平面ABB1A1,A1B1?平面ABB1A1,A1B1∩AA1=A1,
∴A1C1⊥平面ABB1A1.(8分)
∵B1D?平面ABB1A1,∴A1C1⊥B1D.(9分)
又∵B1D⊥A1F,A1C1?平面A1C1F,A1F?平面A1C1F,A1C1∩A1F=A1,
∴B1D⊥平面A1C1F.(11分)
∵直线B1D?平面B1DE,∴平面B1DE⊥平面A1C1F.(12分)
点评 本题三棱锥的体积的求法,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 短期培训 | 长期培训 | 合计 | |
| 能力优秀 | 8 | 54 | 62 |
| 能力不优秀 | 17 | 21 | 38 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | -$\frac{1}{2}+\frac{1}{2}i$ | C. | -$\frac{1}{2}-\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com