
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,易知点
,易知点![]() 为
为![]() 的外接圆圆心,从而
的外接圆圆心,从而![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面ABC;
平面ABC;
(2)以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系, 求出平面
轴建立如图所示的空间直角坐标系, 求出平面![]() 与平面
与平面![]() 的法向量,代入公式即可建立
的法向量,代入公式即可建立![]() 的方程,解之即可.
的方程,解之即可.
(1)证明:如图,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
由题意,得![]() ,则
,则![]() 为直角三角形,
为直角三角形,
点![]() 为
为![]() 的外接圆圆心.
的外接圆圆心.
又点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() 的外接圆圆心,
的外接圆圆心,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:由(1)可知![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
于是以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
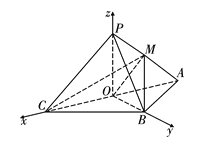
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则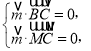 得
得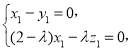
令![]() ,得
,得![]() ,
,![]() ,
,
即![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由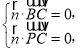 得
得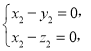
令![]() ,得
,得![]() ,
,![]() ,即
,即![]()
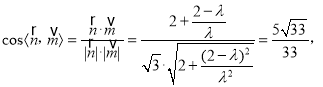
解得![]() 即M为PA的中点.
即M为PA的中点.


科目:高中数学 来源: 题型:
【题目】数学老师给出一个函数![]() ,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在
,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在![]() 上函数单调递减;乙:在
上函数单调递减;乙:在![]() 上函数单调递增;丙:在定义域R上函数的图象关于直线
上函数单调递增;丙:在定义域R上函数的图象关于直线![]() 对称;丁:
对称;丁:![]() 不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,已知:a5=2a2+3且a2,![]() ,a14成等比数列.
,a14成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设正项数列{bn}满足bn2Sn+1=Sn+1+2,求证:b1+b2+…+bn<n+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某省的高考改革方案,考生应在3门理科学科(物理、化学、生物)和3门文科学科(历史、政治、地理)的6门学科中选择3门学科参加考试.根据以往统计资料,1位同学选择生物的概率为0.5,选择物理但不选择生物的概率为0.2,考生选择各门学科是相互独立的.
(1)求1位考生至少选择生物、物理两门学科中的1门的概率;
(2)某校高二段400名学生中,选择生物但不选择物理的人数为140,求1位考生同时选择生物、物理两门学科的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,设O为AC1与A1C的交点,点P为BC的中点.求证:
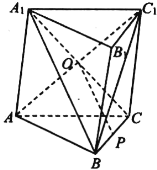
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠(本次即第一次),标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 12 | 4 | 4 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人发放纪念品,求抽到的2人中恰有1人体检3次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com