
【题目】已知椭圆![]() 的离心率
的离心率![]() ,椭圆上的点到左焦点
,椭圆上的点到左焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.在
两点.在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 且
且![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
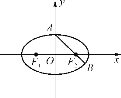
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有一组圆![]() .下列四个命题正确的是( )
.下列四个命题正确的是( )
A. 存在![]() ,使圆与
,使圆与![]() 轴相切
轴相切
B. 存在一条直线与所有的圆均相交
C. 存在一条直线与所有的圆均不相交
D. 所有的圆均不经过原点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海产品经销商调查发现,该海产品每售出![]() 吨可获利
吨可获利![]() 万元,每积压
万元,每积压![]() 吨则亏损
吨则亏损![]() 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
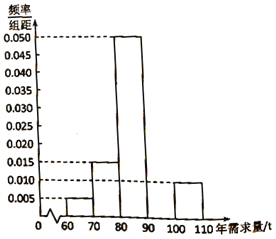
(1)请补齐![]() 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示为
表示为![]() 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).![]() 年
年![]() 月
月![]() 日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年
日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年![]() 元.税率与速算扣除数见下表.
元.税率与速算扣除数见下表.
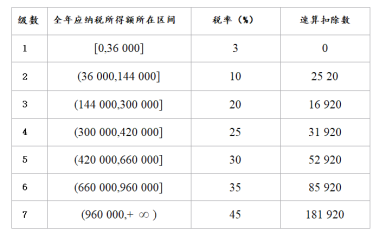
(1)设全年应纳税所得额为![]() ,应缴纳个税税额为
,应缴纳个税税额为![]() ,求
,求![]() 的解析式;
的解析式;
(2)小李全年综合所得收入额为![]() 元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是
元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是
,专项附加扣除是![]() 元,依法确定其他扣除是
元,依法确定其他扣除是![]() 元,那么他全年应缴纳多少综合所得个税?
元,那么他全年应缴纳多少综合所得个税?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种药物在血液中以每小时![]() 的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
![]() 与x的关系式为______;
与x的关系式为______;
![]() 当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时
当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时![]() 精确到
精确到![]() .
.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com