
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为菱形,且
为菱形,且![]() ,
,![]() 为
为![]() 的中点.
的中点.
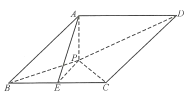
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据菱形基本性质得BC⊥AE,再由线面垂直得BC⊥AP,故BC⊥平面PAE;
(2)以P为坐标原点,![]() 的方向分别为x,y,z轴建立空间直角坐标系,分别求出平面BAP与平面CDP的法向量计算即可.
的方向分别为x,y,z轴建立空间直角坐标系,分别求出平面BAP与平面CDP的法向量计算即可.
(1)连接AC,因为底面ABCD为菱形,且∠ABC=60°,所以△ABC为正三角形,
因为E为BC的中点,所以BC⊥AE,又因为AP⊥平面PBC,BC平面PBC,
所以BC⊥AP,因为AP∩AE=A,AP,AE平面PAE,所以BC⊥平面PAE;
(2)因为AP⊥平面PBC,PB平面PBC,所以AP⊥PB,又因为AB=2,PA=1,所以PB=![]() ,
,
由(1)得BC⊥PE,又因为E为BC中点,所以PB=PC=![]() ,EC=1,所以PE=
,EC=1,所以PE=![]() ,
,
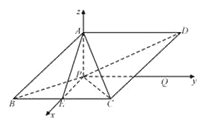
如图,过点P作BC的平行线PQ,则PQ,PE,PA两两互相垂直,
以P为坐标原点,![]() 的方向分别为x,y,z轴建立如图所示的空间直角坐标系,
的方向分别为x,y,z轴建立如图所示的空间直角坐标系,
则P(0,0,0),A(0,0,1),B(![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,1),
,1,0),D(0,2,1),
设平面BAP的一个法向量![]() =(x,y,z),又
=(x,y,z),又![]() =(0,0,1),
=(0,0,1),![]() =(
=(![]() ,﹣1,0),
,﹣1,0),
由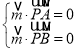 ,得
,得![]() x﹣y=0,z=0,令x=1,则
x﹣y=0,z=0,令x=1,则![]() =(1,
=(1,![]() ,0),
,0),
设平面CDP的一个法向量![]() =(a,b,c),又
=(a,b,c),又![]() =(
=(![]() ,1,0),
,1,0),![]() =(0,2,1),
=(0,2,1),
由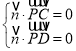 ,得
,得![]() a+b=0,2y+z=0,令a=1,则
a+b=0,2y+z=0,令a=1,则![]() =(1,﹣
=(1,﹣![]() ,2
,2![]() ),
),
所以![]() ,即平面ABP与平面CDP所成锐二面角的余弦值为
,即平面ABP与平面CDP所成锐二面角的余弦值为![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知![]() ,
,![]() ,Q到海岸线OM,ON的距离分别为3 km,
,Q到海岸线OM,ON的距离分别为3 km,![]() km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
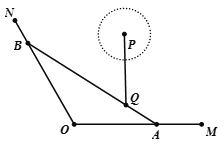
(1)求水上旅游线AB的长;
(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为![]() (a为大于零的常数).强水波开始生成时,一游轮以
(a为大于零的常数).强水波开始生成时,一游轮以![]() km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,线段BC的端点
中,线段BC的端点![]() 分别在边
分别在边![]() 、
、![]() 上滑动,且
上滑动,且![]() ,现将
,现将![]() ,
,![]() 分别沿AB,AC折起使点
分别沿AB,AC折起使点![]() 重合,重合后记为点
重合,重合后记为点![]() ,得到三被锥
,得到三被锥![]() .现有以下结论:
.现有以下结论:
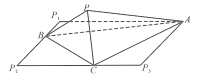
①![]() 平面
平面![]() ;
;
②当![]() 分别为
分别为![]() 、
、![]() 的中点时,三棱锥
的中点时,三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() ;
;
③![]() 的取值范围为
的取值范围为![]() ;
;
④三棱锥![]() 体积的最大值为
体积的最大值为![]() .
.
则正确的结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金石文化,是中国悠久文化之一.“金”是指“铜”,“石”是指“石头”,“金石文化”是指在铜器或石头上刻有文字的器件.在一千多年前,有一种凸多面体工艺品,是金石文化的代表作,此工艺品的三视图是三个全等的正八边形(如图),若一个三视图(即一个正八边形)的面积是![]() ,则该工艺品共有______个面,表面积是______.
,则该工艺品共有______个面,表面积是______.
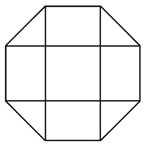
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有下列四个结论,其中所有正确结论的编号是___________.
①若![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差数列
是等差数列![]() 的前
的前![]() 项,则
项,则![]() ;
;
③“![]() ”的一个必要不充分条件是“
”的一个必要不充分条件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com