
【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3 ![]() km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= ![]() ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
【答案】
(1)解:在△AOM中,A0=15,∠AOM=β,且cosβ= ![]() ,OM=3
,OM=3 ![]() ,
,
由余弦定理可得:AM2=OA2+OM2﹣2OAOMcos∠AOM=(3 ![]() )2+152﹣2×
)2+152﹣2× ![]() ×15×
×15× ![]() =72.
=72.
所以可得:AM=6 ![]() ,大学M在站A的距离AM为6
,大学M在站A的距离AM为6 ![]() km
km
(2)解:∵cos ![]() ,且β为锐角,∴sinβ=
,且β为锐角,∴sinβ= ![]() ,
,
在△AOM中,由正弦定理可得: ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,∴sin∠MAO=
,∴sin∠MAO= ![]() ,
,
∴∠MAO= ![]() ,∴∠ABO=α﹣
,∴∠ABO=α﹣ ![]() ,
,
∵tanα=2,∴sin ![]() ,cosα=
,cosα= ![]() ,
,
∴sin∠ABO=sin( ![]() )=
)= ![]() ,
,
又∵∠AOB=π﹣α,∴sin∠AOB=sin(π﹣α)= ![]() .
.
在△AOB中,AO=15,由正弦定理可得: ![]() =
= ![]() ,即
,即 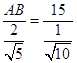 ,∴解得AB=30
,∴解得AB=30 ![]() ,即铁路AB段的长AB为30
,即铁路AB段的长AB为30 ![]() km
km
【解析】(1)在△AOM中,利用已知及余弦定理即可解得AM的值;(2)由cos ![]() ,且β为锐角,可求sinβ,由正弦定理可得sin∠MAO,结合tanα=2,可求sinα,cosα,sin∠ABO,sin∠AOB,结合AO=15,由正弦定理即可解得AB的值.
,且β为锐角,可求sinβ,由正弦定理可得sin∠MAO,结合tanα=2,可求sinα,cosα,sin∠ABO,sin∠AOB,结合AO=15,由正弦定理即可解得AB的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x) ![]() (x+1)2恒成立.
(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2(a为实常数).
(1)当a=﹣4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1 , x2∈[1,e],都有 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中
(其中![]() 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() +
+ ![]() =1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4
=1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4 ![]() .
.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点.以AB为底作等腰三角形,顶点为P(﹣3,2),求△PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com