
【题目】排成一排的10名学生生日的月份均不相同.有![]() 名教师,依次挑选这些学生参加
名教师,依次挑选这些学生参加![]() 个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求
个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求![]() 的最小值.
的最小值.
【答案】4
【解析】
若![]() ,不妨设这10名学生生日的月份分别为
,不妨设这10名学生生日的月份分别为![]() .
.
当学生按生日排序为4,3,2,1,7,6,5,9,8,10时,存在一名教师至少要挑选前四名学生中的两名,由于这两名学生生日的月份是逐渐减少的,且后六名学生生日的月份均大于前四名学生生日的月份,因此,这名教师不可能再挑选后六名学生;在余下的不超过两名教师中,一定存在一名教师至少要挑选第五名至第七名学生中的两名.同理,这名教师不可能再挑选后三名学生;余下的不超过一名教师也不可能挑选后三名学生,矛盾.
下面证明:对于互不相同的有序实数列![]() ,当
,当![]() 时,一定存在三个数
时,一定存在三个数![]() 满足
满足![]() 或
或![]() .
.
设最大数、最小数分别为![]() 、
、![]() .
.
不妨设![]() .
.
若![]() ,则
,则![]() 满足
满足![]() ;
;![]() .
.
因为![]() ,所以,要么在
,所以,要么在![]() 的前面,要么在
的前面,要么在![]() 的后面至少有两个数.
的后面至少有两个数.
不妨设在![]() 的后面有两个数
的后面有两个数![]() .从而,
.从而,![]() 与
与![]() 中一定有一个成立.
中一定有一个成立.
引用上面的结论,当![]() 时,第一名教师至少可以挑选3名学生;若余下的学生大于或等于5名,则第二名教师也至少可以挑选3名学生;这时,剩下的学生的数目不超过4名,可以被两名教师全部挑选.
时,第一名教师至少可以挑选3名学生;若余下的学生大于或等于5名,则第二名教师也至少可以挑选3名学生;这时,剩下的学生的数目不超过4名,可以被两名教师全部挑选.
因此,![]() 的最小值为4.
的最小值为4.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: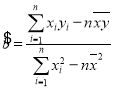 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数集合![]() ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素![]() 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“可分集合”.
为“可分集合”.
(1)判断集合![]() 和
和![]() 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);
(2)求证:五个元素的集合![]() 一定不是“可分集合”;
一定不是“可分集合”;
(3)若集合![]() 是“可分集合”.
是“可分集合”.
①证明:![]() 为奇数;
为奇数;
②求集合![]() 中元素个数的最小值.
中元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图椭圆![]() 的离心率为
的离心率为![]() , 其左顶点
, 其左顶点![]() 在圆
在圆![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,与圆
,与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在直线
.是否存在直线![]() ,使得
,使得![]() ? 若存在,求出直线
? 若存在,求出直线![]() 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=![]() AD,E是线段PD上的点,F是线段AB上的点,
AD,E是线段PD上的点,F是线段AB上的点,
且![]() .
.
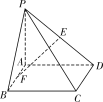
(1)证明:EF∥平面PBC;
(2)是否存在实数λ,使得异面直线EF与CD所成角为60°?若存在,试求出λ的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com