
【题目】已知数列![]() 的前n项和
的前n项和![]() .求:
.求:
(I)求数列![]() 的通项公式;
的通项公式;
(II)求数列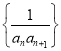 的前n项和
的前n项和![]() ;
;
(III)求![]() 的最小值.
的最小值.
【答案】(Ⅰ) 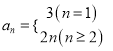 ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(1)先求出![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() ,两式相减,验证当
,两式相减,验证当![]() 时是否成立,即可得到数列
时是否成立,即可得到数列![]() 的通项公式;(
的通项公式;(![]() )由(1)可得
)由(1)可得![]() ,利用裂项相消法求解即可;(
,利用裂项相消法求解即可;(![]() )由(1)可得
)由(1)可得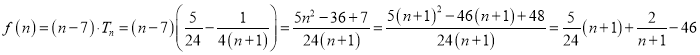 ,利用基本不等式,结合
,利用基本不等式,结合![]() 是正整数,即可得结果.
是正整数,即可得结果.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
两式相减得![]() ,
,
经验证![]() 不满足上式.
不满足上式.
故![]() .
.
(![]() )当
)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]()
![]() .
.
经检验![]() 满足上式,故
满足上式,故![]() .
.
(![]() )
)
![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
∵![]() ,求
,求![]() ,
, ![]() ,
,
∴当![]() 时,
时, ![]() 取最小值,
取最小值, ![]() .
.
【方法点晴】本题主要考查等差数列的通项与基本不等式求最值,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
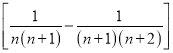 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为x,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函数f(x)的最小正周期为π.
ωx)(ω>0),且函数f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,

(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.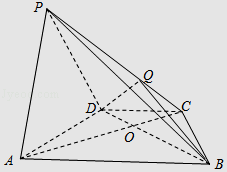
(1)求证:PA∥平面QBD;
(2)求证BD⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据中点坐标公式求出![]() 中点
中点![]() 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得![]() 的斜率,利用点斜式可求
的斜率,利用点斜式可求![]() 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出![]() 的斜率,从而求出
的斜率,从而求出![]() 边上的高所在直线的斜率为
边上的高所在直线的斜率为![]() ,利用点斜式可求
,利用点斜式可求![]() 边上的高所在直线的方程.
边上的高所在直线的方程.
试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=![]() =8,
=8,
所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=![]() =1,
=1,
所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜![]() ,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜
,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜![]() 之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
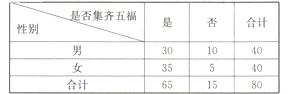
(1)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(2)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com