
【题目】设函数![]() ,
,![]()
(1) 若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2) 若函数![]() 有两个零点,求实数a的取值范围.
有两个零点,求实数a的取值范围.
【答案】(1)函数![]() 的增区间为(0,1),减区间为
的增区间为(0,1),减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出函数的导数,判断正负求出函数的单调区间即可;
(2)求![]() ,
, ![]() 讨论
讨论![]()
![]() 的单调性进而确定函数
的单调性进而确定函数![]() 的零点个数即可求解
的零点个数即可求解
(1)f(x)的定义域为(0,+∞),![]()
若![]() ,
,![]() ,故
,故![]()
当![]() 则函数
则函数![]() 的增区间为(0,1),减区间为
的增区间为(0,1),减区间为![]() ;
;
(2)![]() ,且
,且![]()
![]()
当![]() 则)
则)![]() ,则
,则![]() 至多有一个零点,不合题意;
至多有一个零点,不合题意;
当![]() ,
,![]() 当
当![]() ,
,![]()
① 当![]() 即
即![]() 时,
时,![]() 故
故![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,则
上单调递减,则![]() ,又
,又![]() 又
又![]() ,则
,则![]()
则![]() 则在
则在![]() 上
上![]() 单调递增,在
单调递增,在![]()
![]() 单调递减,在
单调递减,在![]()
![]() 单调递增,又
单调递增,又![]() ,则若函数
,则若函数![]() 有两个零点,只需
有两个零点,只需![]() ,综上
,综上![]() ;
;
② 当![]() 即
即![]() 时,
时,![]() 故
故![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,则
上单调递减,则![]() ,又
,又![]() 又
又![]() ,则
,则![]()
则![]() 则在
则在![]() 上
上![]() 单调递增,在
单调递增,在![]()
![]() 单调递减,在
单调递减,在![]()
![]() 单调递增,又
单调递增,又![]() ,则函数
,则函数![]() 必有两个零点,故
必有两个零点,故![]() ,
,
③当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,易得
,易得![]() 的极大值也就是最大值为
的极大值也就是最大值为![]() ,则
,则![]() ,由
,由![]() ,函数有唯一零点1,不合题意
,函数有唯一零点1,不合题意
综上实数a的取值范围.![]()


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】数列![]() 满足:对一切
满足:对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列上有界(有上界),并称
无关的常数,称数列上有界(有上界),并称![]() 是它的一个上界,对一切
是它的一个上界,对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列下有界(有下界),并称
无关的常数,称数列下有界(有下界),并称![]() 是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设
是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若数列![]() 为常数列,试求实数
为常数列,试求实数![]() 、
、![]() 满足的等式关系,并求出实数
满足的等式关系,并求出实数![]() 的取值范围;
的取值范围;
(2)下面四个选项,对一切实数![]() ,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
A. 当![]() 时,
时,![]() B. 当
B. 当![]() 时,
时,![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
(3)若![]() ,
,![]() ,且数列
,且数列![]() 是有界数列,求
是有界数列,求![]() 的值及
的值及![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,满足
,满足![]() . 数列
. 数列![]() 的首项为
的首项为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记集合![]() ,若集合
,若集合![]() 的元素个数为
的元素个数为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() 使得
使得![]() 成立?如果存在,请写出
成立?如果存在,请写出![]() 满足的条件,如果不存在,请说明理由.
满足的条件,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将向量![]() =(
=(![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ),…
),…![]() =(
=(![]() ,
,![]() )组成的系列称为向量列{
)组成的系列称为向量列{![]() },并定义向量列{
},并定义向量列{![]() }的前
}的前![]() 项和
项和![]() .如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{
.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{![]() }是等差向量列,那么下述四个向量中,与
}是等差向量列,那么下述四个向量中,与![]() 一定平行的向量是 ( )
一定平行的向量是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)为了解该种蛋糕的市场需求情况与性別是否有关,随机统计了100人的购买情况,得如下列联表:
男 | 女 | 合计 | |
购买 | 15 | 35 | 50 |
不购买 | 6 | 44 | 50 |
合计 | 21 | 79 | 100 |
问:能否有![]() 的把握认为是否购买蛋糕与性別有关?
的把握认为是否购买蛋糕与性別有关?
附: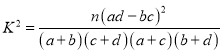
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com