
【题目】已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() ;
;
(1)试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,记
,记![]() (其中
(其中![]() 为整数集),若集合
为整数集),若集合![]() 为有限集,求实数
为有限集,求实数![]() 的取值范围,使得集合
的取值范围,使得集合![]() 中元素个数最少,并用列举法表示集合
中元素个数最少,并用列举法表示集合![]() ;
;
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数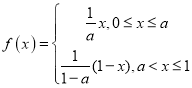 ,其中
,其中![]() 为常数且
为常数且![]() .新定义:若
.新定义:若![]() 满足
满足![]() ,但
,但![]() ,则称
,则称![]() 为
为![]() 的回旋点.
的回旋点.
(1)当![]() 时,分别求
时,分别求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的解析式,并求出
的解析式,并求出![]() 回旋点;
回旋点;
(3)证明函数![]() 在
在![]() 有且仅有两个回旋点,并求出回旋点
有且仅有两个回旋点,并求出回旋点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种排列,在欧洲这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中出现了如图所示的表,这是我国数学史上的一次伟大成就,如图所示,在“杨辉三角”中去除所有为1的项,依次构成数列,2,3,3,4,6,4,5 ,10 ,10,5,……,则此数列的前119项的和为__________.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn(n∈N*),等比数列{bn}的前n项和为Tn(n∈N*),已知a1=3,b1=1,a3+b2=10,S3﹣T2=11.
(Ⅰ)求数列{an}、{bn}的通项公式:
(Ⅱ)若数列{cn}满足c1=1,cn+1﹣cn=an,求c100;
(Ⅲ)设数列dn=anbn,求{dn}的前n项和Kn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C的中心在原点,抛物线![]() 的焦点是双曲线C的一个焦点,且双曲线过点
的焦点是双曲线C的一个焦点,且双曲线过点![]() .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线![]() 与双曲线C交于A,B两点,试问:k为何值时,
与双曲线C交于A,B两点,试问:k为何值时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
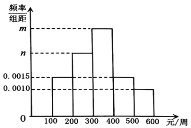
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制右图所示频率分布直方图,已知中间三组的人数可构成等差数列.
(1)求![]() 的值;
的值;
(2)分析人员对抽取对象每周的消费金额y与年龄x进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为22岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为22岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
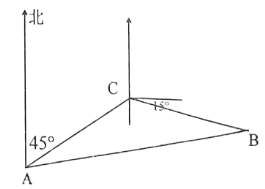
【题目】宿州泗县石龙湖国家湿地公园是保存完好的典型湿地生态系统,具有得天独厚的旅游资源.某日一游船在湖上游玩航行中突然遇险,发出呼救信号,驻湖救援队在![]() 处获悉后,立即测出该游船在北偏东
处获悉后,立即测出该游船在北偏东![]() 方向上,距离
方向上,距离![]() 有
有![]() 千米的
千米的![]() 处,并测得游船正沿东偏南
处,并测得游船正沿东偏南![]() 的方向,以
的方向,以![]() 千米/时的速度向湖心小岛
千米/时的速度向湖心小岛![]() 靠拢,救援舰艇立即以
靠拢,救援舰艇立即以![]() 千米/时的速度前去营救,若想用最短的时间营救游船,求舰艇的航行方向和所需时间.
千米/时的速度前去营救,若想用最短的时间营救游船,求舰艇的航行方向和所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有5个匣子,每个匣子有一把钥匙,并且钥匙不能通用.如果随意在每一个匣内放入一把钥匙,然后把匣子全都锁上.现在允许砸开一个匣子,使得能相继用钥匙打开其余4个匣子,那么钥匙的放法有______种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com