
【题目】已知函数f(x)=![]() .
.
(1)若函数f(x)的图像中相邻两条对称轴间的距离不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若函数f(x)的最小正周期为π,且当x∈![]() 时,f(x)的最大值是
时,f(x)的最大值是![]() ,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
科目:高中数学 来源: 题型:
【题目】如图所示的矩形![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 边上异于
边上异于![]() ,
, ![]() 两点的动点,且
两点的动点,且![]() ,
, ![]() 为线段
为线段![]() 的中点,现沿
的中点,现沿![]() 将四边形
将四边形![]() 折起,使得
折起,使得![]() 与
与![]() 的夹角为
的夹角为![]() ,连接
,连接![]() ,
, ![]() .
.

(1)探究:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,说明点
,若存在,说明点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(2)求三棱锥![]() 的体积的最大值,并计算此时
的体积的最大值,并计算此时![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
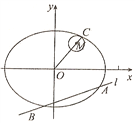
【题目】如图所示,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心在原点,点
的中心在原点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 上一点,圆
上一点,圆![]() 的半径为
的半径为![]() ,且
,且![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》中有如下两个问题:
[三三]今有宛田,下周三十步,径十六步.问为田几何?
[三四]又有宛田,下周九十九步,径五十一步.问为田几何?
翻译为:[三三]现有扇形田,弧长30步,直径长16步.问这块田面积是多少?
[三四]又有一扇形田,弧长99步,直径长51步.问这块田面积是多少?
则下列说法正确的是( )
A.问题[三三]中扇形的面积为240平方步B.问题[三四]中扇形的面积为![]() 平方步
平方步
C.问题[三三]中扇形的面积为60平方步D.问题[三四]中扇形的面积为![]() 平方步
平方步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
B.若三个平面两两相交,其中两个平面的交线与第三个平面平行.则另外两条交线平行;
C.如果![]() 是两条异面直线,那么直线
是两条异面直线,那么直线![]() 一定是异面直线;
一定是异面直线;
D.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 绕
绕![]() 所在直线旋转一周,所形成的几何体的轴截面面积为10.
所在直线旋转一周,所形成的几何体的轴截面面积为10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com