
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,证明:
,证明:![]() ,当
,当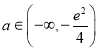 时,函数
时,函数![]() 恒有两个不同零点.
恒有两个不同零点.
【答案】(1)![]() 时,在
时,在![]() 上单调递增;
上单调递增;![]() 时,在
时,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析
上单调递减;(2)证明见解析
【解析】
(1)分别在![]() 和
和![]() 两种情况下讨论导函数的正负,从而得到原函数的单调性;
两种情况下讨论导函数的正负,从而得到原函数的单调性;
(2)将问题转化为当 时,
时,![]() 与
与![]() 恒有两个不同的交点的证明;利用导数可求得
恒有两个不同的交点的证明;利用导数可求得![]() 的单调性和最值,从而确定
的单调性和最值,从而确定![]() 的范围,解得
的范围,解得![]() 的范围.
的范围.
(1)由题意得:![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由题意得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,则问题等价于当
,则问题等价于当 时,
时,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() ,又
,又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
即 ,
,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
![]() 当
当 时,
时,![]() 在
在![]() 上恒有两个不同的零点.
上恒有两个不同的零点.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图中实线所示,图中圆C与
)的部分图象如图中实线所示,图中圆C与![]() 的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )
的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )

A.函数![]() 的最小正周期是2π
的最小正周期是2π
B.函数![]() 的图象关于点
的图象关于点![]() 成中心对称
成中心对称
C.函数![]() 在
在![]() 单调递增
单调递增
D.将函数![]() 的图象向左平移
的图象向左平移![]() 后得到的关于y轴对称
后得到的关于y轴对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以轴正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 分别交于异于极点O的四点A,B,C,D.
分别交于异于极点O的四点A,B,C,D.
(1)若曲线![]() 关于
关于![]() 对称,求
对称,求![]() 的值,并求
的值,并求![]() 的参数方程;
的参数方程;
(2)若![]() |,当
|,当![]() 时,求
时,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用计算机生成随机数表模拟预测未来三天降雨情况,规定1,2,3表示降雨,4,5,6,7,8,9表示不降雨,根据随机生成的10组三位数:654 439 565 918 288 674 374 968 224 337,则预计未来三天仅有一天降雨的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到:任画…条线段,然后把它分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了由4条小线段构成的折线,称为“一次构造”;用同样的方法把每一条小线段重复上述步骤,得到由16条更小的线段构成的折线,称为“二次构造”;…;如此进行“n次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度大于初始线段的100倍,则至少需要构造的次数是( )(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】滕州市公交公司一切为了市民着想,为方便市区学生的上下学,专门开通了学生公交专线,在学生上学、放学的时间段运行,为了更好地掌握发车间隔时间,公司工作人员对滕州二中车站发车间隔时间与侯车人数之间的关系进行了调查研究,现得到如下数据:
间隔时间 | 10 | 11 | 13 | 12 | 15 | 14 |
侯车人数 | 23 | 25 | 29 | 26 | 31 | 28 |
调查小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据不相邻的概率;
(2)若选取的是前两组数据,请根据后四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的差均不超过1人,则称为最佳回归方程,在(2)中求出的回归方程是否是最佳回归方程?若规定一辆公交车的载客人数不超过35人,则间隔时间设置为18分钟,是否合适?
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,在
,在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 轴分别交
轴分别交![]() 于点
于点![]() .当
.当![]() ,直线
,直线![]() 的斜率为1时,
的斜率为1时,![]() .
.

(1)求抛物线的方程;
(2)判断![]() 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com