
分析 (1)直接利用有理指数幂的运算法则化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 (1)解:$\root{4}{{{{(3-π)}^4}}}+{({0.008})^{-\frac{1}{3}}}-{({0.25})^{\frac{1}{2}}}×{({\frac{1}{{\sqrt{2}}}})^{-4}}$=π-3+(0.2)-1-$\frac{1}{2}×4$=π …(7分)
(2)解:$\frac{1}{2}lg\frac{32}{49}-\frac{4}{3}lg\sqrt{8}+lg\sqrt{245}+{2}^{1+{log}_{2}3}$=$\frac{1}{2}(5lg2-2lg7)-lg2+\frac{1}{2}(lg5+2lg7)$+2×3=$\frac{1}{2}(4lg2+1)-2lg2+$=$\frac{13}{2}$ …(14分)
点评 本题考查有理指数幂的运算法则以及对数运算法则的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=$\frac{π}{3}$,OA⊥底面ABCD,OA=2,M为OA的中点.求点B到平面OCD的距离.
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=$\frac{π}{3}$,OA⊥底面ABCD,OA=2,M为OA的中点.求点B到平面OCD的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$+1 | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{16}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
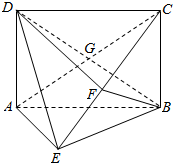 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com