
 与
与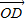 垂直,求实数t的值.
垂直,求实数t的值.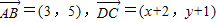 ,由四边形ABCD是平行四边形,知
,由四边形ABCD是平行四边形,知 ,解得C(1,4).由此能求出两条对角线AC,BD的长度.
,解得C(1,4).由此能求出两条对角线AC,BD的长度.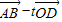 =(3,5)-(-2t,-t)=(3+2t,5+t),
=(3,5)-(-2t,-t)=(3+2t,5+t),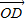 =(-2,-1),向量
=(-2,-1),向量 与
与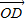 垂直,知(3+2t,5+t)•(-2,-1)=0,由此能求出t.
垂直,知(3+2t,5+t)•(-2,-1)=0,由此能求出t. ,
,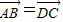 ,
, ,解得x=1,y=4.即C(1,4).
,解得x=1,y=4.即C(1,4).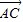 =(2,6),AC的长度
=(2,6),AC的长度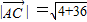 =2
=2 ,
,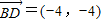 ,BD的长度
,BD的长度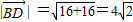 .
.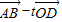 =(3,5)-(-2t,-t)=(3+2t,5+t),
=(3,5)-(-2t,-t)=(3+2t,5+t), =(-2,-1),
=(-2,-1), 与
与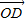 垂直,
垂直, .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:
| AB |
| OD |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=
如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=| 2-2cos2 | ||
|
| 2-2cos2 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
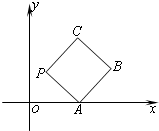 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k,4k+2],k∈z [4k,4k+2],k∈z |
| 递减区间 | [4k-2,4k],k∈z [4k-2,4k],k∈z | |
| 零点 | x=4k,k∈z x=4k,k∈z | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com