
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 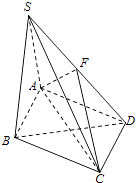
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
【答案】
(1)解:由题意,三棱锥S﹣FAC的体积=三棱锥S﹣DAC的体积的一半.
取AB的中点O,连接SO,则SO⊥底面ABCD,SO= ![]() ,
,
∵S△DAC= ![]() =
= ![]() ,
,
∴三棱锥S﹣FAC的体积= ![]() =
= ![]()
(2)解:连接OD,OC,则OC=OD= ![]() ,∴SC=SD=3,
,∴SC=SD=3,
△SAD中,SA=AD=2,F为SD的中点,∴AF= ![]() =
= ![]() .
.
△SCD中,SC=SD=3,CD=2,∴9+4CF2=2(9+4),∴CF= ![]() ,
,
△FAC中,cos∠AFC= 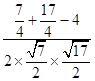 =
= ![]() ,
,
∴sin∠AFC= ![]() ,
,
∴S△AFC= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]()
设D到平面AFC的距离为h,则 ![]() ,∴h=
,∴h= ![]() ,
,
∴直线BD与平面FAC所成角的正弦值 ![]() ÷
÷ ![]() =
= ![]()
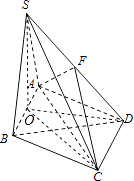
【解析】(1)由题意,三棱锥S﹣FAC的体积=三棱锥S﹣DAC的体积的一半,取AB的中点O,连接SA,利用体积公式求三棱锥S﹣FAC的体积;(2)求出D到平面AFC的距离,即可求直线BD与平面FAC所成角的正弦值.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则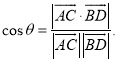 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .建立如图所示的空间直角坐标系.
.建立如图所示的空间直角坐标系.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 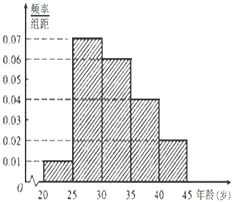
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
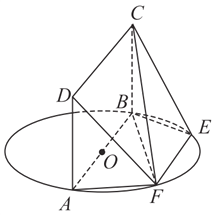
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中: ①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )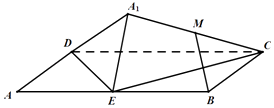
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() ,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
(1)若椭圆C过点 ,且右准线方程为
,且右准线方程为![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)若直线BN的斜率是直线AM斜率的2倍,求椭圆C的离心率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com