练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知关于的方程有两个不同的实数根、.

    （Ⅰ）求实数的取值范围；

    （Ⅱ）求证：.

    【答案】（I）；（II）证明见解析.

    【解析】

    试题分析：（1）方程有两个不同的实数根、，等价于有两个不等根，对函数求导，使得函数的图象与有两个不同的交点即可;(2) 证，只需证，需证，构造函数证明大于0.

    解析：

    （Ⅰ）∵，∴.令，

    则 ，

    令，解得，令，解得，

    则函数在上单调递增，在上单调递减，

    ∴；

    又当时，，当时，，

    画出函数的图象.

    要使函数的图象与有两个不同的交点，

    则，即实数的取值范围为.

    （Ⅱ）由（Ⅰ）知，，不妨设，则，.

    要证，只需证.

    ∵，且函数在上单调递减，

    ∴只需证，又，∴只需证，

    即证，即证对恒成立.

    令，，则，

    ∵，∴，∴恒成立，

    则函数在上单调递减，∴.

    综上所述，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】

    已知椭圆.过点（m,0）作圆的切线l交椭圆G于A，B两点.

    （I）求椭圆G的焦点坐标和离心率；

    （II）将表示为m的函数，并求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司计划投资A、B两种金融产品，根据市场调查与预测，A产品的利润与投资量的算术平方根成正比例，其关系如图1，B产品的利润与投资量成正比例，其关系如图2(注：利润与投资量的单位：万元)．

    （1）分别将A、B两产品的利润表示为投资量的函数关系式；

    （2）该公司已有10万元资金，并全部投入A、B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在直三棱柱中，，，，，，点在线段上.

    （Ⅰ）证明：；

    （Ⅱ）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC中，A(0,1)，AB边上的高CD所在直线的方程为x＋2y－4＝0，AC边上的中线BE所在直线的方程为2x＋y－3＝0.

    (1)求直线AB的方程；

    (2)求直线BC的方程；

    (3)求△BDE的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为奇函数， 为偶函数，且．

    （1）求及的解析式及定义域；

    （2）若关于的不等式恒成立，求实数的取值范围．

    （3）如果函数，若函数有两个零点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市100户居民的月平均用电量(单位：度)以[160，180)[180，200)[200，220)[220，240)[240，260)[260，280)[280，300)分组的频率分布直方图如图所示：

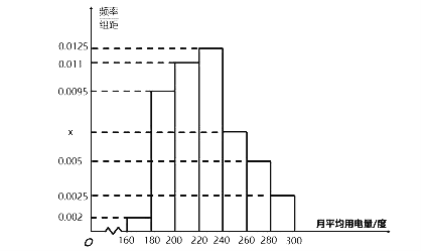
    （1）求直方图中的值；

    （2）用分层抽样的方法从[260，280)和[280，300)这两组用户中确定6人做随访，再从这6人中随机抽取2人做问卷调查，则这2人来自不同组的概率是多少？

    （3）求月平均用电量的众数和中位数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线C的极坐标方程为.

    （1）求曲线的普通方程和的直角坐标方程；

    （2）设分别交于点，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：k2﹣8k﹣20≤0，命题q：方程1表示焦点在x轴上的双曲线．

    （1）命题q为真命题，求实数k的取值范围；

    （2）若命题“p∨q”为真，命题“p∧q”为假，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案