
【题目】已知左、右焦点分别为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程。
(II)圆![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线
与椭圆C交于A,B两点,R为线段AB上任一点,直线![]() 交椭圆C于P,Q两点,若AB为圆
交椭圆C于P,Q两点,若AB为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于1,求
的斜率大于1,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)利用椭圆C过点![]() ,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.
,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.
(Ⅱ)设A(![]() ),B(
),B(![]() ),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立
),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立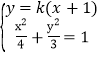 ,设P(x3,y3),Q(x4,y4),利用韦达定理,结合
,设P(x3,y3),Q(x4,y4),利用韦达定理,结合![]() ,
,![]() ,化简|PF1||QF1|,通过
,化简|PF1||QF1|,通过![]() ,求解|PF1||QF1|的取值范围.
,求解|PF1||QF1|的取值范围.
(Ⅰ)∵椭圆![]() 过点
过点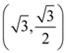 ,∴
,∴![]() ,①
,①
∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,②
,②
由①②得![]() ,
,![]() ,
,
∴椭圆![]() 的离心率
的离心率![]() ,标准方程为
,标准方程为![]() .
.
(Ⅱ)因为![]() 为圆
为圆![]() 的直径,所以点
的直径,所以点![]()
![]() 为线段
为线段![]() 的中点,
的中点,
设![]() ,
,![]() ,则,
,则,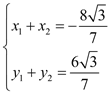 ,又
,又 ,
,
所以![]() ,则
,则![]() ,故
,故![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() .代入椭圆
.代入椭圆![]() 的方程并整理得
的方程并整理得![]() ,
,
则![]() ,故直线
,故直线![]() 的斜率
的斜率![]() .
.
设![]() ,由
,由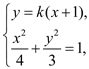 ,得
,得![]() ,
,
设![]() ,
,![]() ,则有
,则有![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
所以![]()
![]() =
=![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为一等品;指标在区间
的为一等品;指标在区间![]() 的为二等品,现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
的为二等品,现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
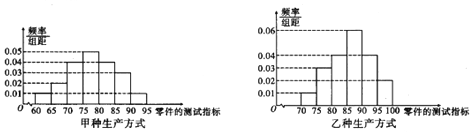
![]() 若从甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取5件,再从这5件零件中随机抽取3件,求至少有1件一等品的概率;
若从甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取5件,再从这5件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 该厂所生产这种零件,若是一等品每件可售50元,若是二等品每件可售20元
该厂所生产这种零件,若是一等品每件可售50元,若是二等品每件可售20元![]() 甲种生产方式每生产一件零件
甲种生产方式每生产一件零件![]() 无论是一等品还是二等品
无论是一等品还是二等品![]() 的成本为10元,乙种生产方式每生产一件零件
的成本为10元,乙种生产方式每生产一件零件![]() 无论是一等品还是二等品
无论是一等品还是二等品![]() 的成本为18元
的成本为18元![]() 将频率分布直方图中的频率视作概率,用样本估计总体比较在甲、乙两种不同生产方式下,哪种生产方式生产的零件所获得的平均利润较高?
将频率分布直方图中的频率视作概率,用样本估计总体比较在甲、乙两种不同生产方式下,哪种生产方式生产的零件所获得的平均利润较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有
A. 72种 B. 36种 C. 24种 D. 18种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,
上,![]() 为坐标原点,
为坐标原点,![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过焦点![]() ,且斜率为1的直线
,且斜率为1的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线
的垂直平分线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为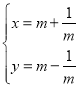 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校体育教研组研发了一项新的课外活动项目,为了解该项目受欢迎程度,在某班男女中各随机抽取20名学生进行调研,统计得到如下列联表:

附:参考公式及数据![]()
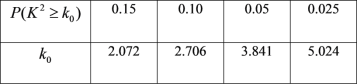
(1)在喜欢这项课外活动项目的学生中任选1人,求选到男生的概率;
(2)根据题目要求,完成2×2列联表,并判断是否有95%的把握认为“喜欢该活动项目与性别有关”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为抛物线
为抛物线![]() 上一点,斜率分别为
上一点,斜率分别为![]() ,
,![]()
![]() 的直线PA,PB分别交抛物线于点A,B(不与点P重合).
的直线PA,PB分别交抛物线于点A,B(不与点P重合).

(1)证明:直线AB的斜率为定值;
(2)若△ABP的内切圆半径为![]() .
.
(i)求△ABP的周长(用k表示);
(ii)求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com