
(10分)用斜二测画法画底面半径为2 cm,高为3 cm的圆锥的直观图.
(1)以底面圆心O为原点建立直角坐标系xOy,并每隔0.5cm作圆的平行于y轴的弦作为辅助线,如图①.
(2)建立x′O′y′水平面,使∠x′O′y′=45°,画出底面圆的直观图如图②,此时A′B′="4" cm,C′D′="2" cm.?(3)过O′作z′轴,使∠x′O′z′=90°,在z′轴上取一点V′,使O′V′=3cm,连结V′A′、V′B′去掉坐标系及辅助线就得到所求圆锥的直观图.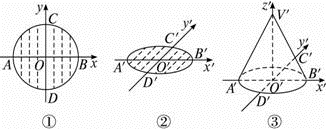
解析试题分析:(1)以底面圆心O为原点建立直角坐标系xOy,并每隔0.5cm作圆的平行于y轴的弦作为辅助线,如图①.
(2)建立x′O′y′水平面,使∠x′O′y′=45°,画出底面圆的直观图如图②,此时A′B′="4" cm,C′D′="2" cm.
(3)过O′作z′轴,使∠x′O′z′=90°,在z′轴上取一点V′,使O′V′=3cm,连结V′A′、V′B′去掉坐标系及辅助线就得到所求圆锥的直观图.
考点:斜二测画法。
点评:在斜二测画法中,要注意平行于y轴和平行于z轴的线段的距离的变化。


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥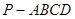 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面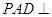 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.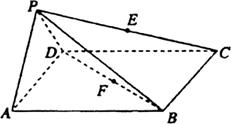
(1)求证: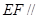 平面PAD;
平面PAD;
(2)求证:平面PDC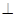 平面PAD;
平面PAD;
(3)求四棱锥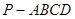 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)如图,在长方体ABCD-A1B1C1D1中,E, F分别是棱BC,CC1上的点,CF="AB=2CE," AB:AD:AA1=1:2:4.
(Ⅰ)求异面直线EF与A1D所成角的余弦值;
(Ⅱ)证明AF⊥平面A1ED;
(Ⅲ)求二面角A1-ED-F的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
如图,在四棱锥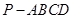 中,底面
中,底面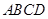 是矩形,
是矩形,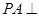 平面
平面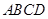 ,
,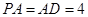 ,
,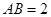 .以
.以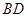 的中点
的中点 为球心、
为球心、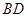 为直径的球面切
为直径的球面切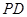 于点
于点 .
.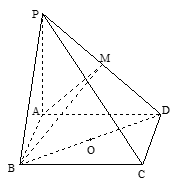
(1)求证:PD⊥平面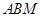 ;
;
(2)求直线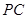 与平面
与平面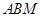 所成的角的正弦值;
所成的角的正弦值;
(3)求点 到平面
到平面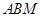 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
正方体ABCD-A1B1C1D1中,E、G分别是BC、C1D1的中点,如图所示.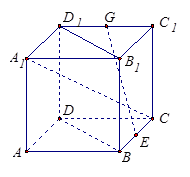
(1)求证:BD⊥A1C;
(2)求证:EG∥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.试探究点M的位置,使F—AE—M为直二面角.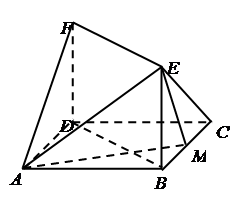
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com