
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线斜率为1,求函数
处的切线斜率为1,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)在R上单调递增;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)根据曲线![]() 在点
在点![]() 处的切线斜率为1,可求出参数
处的切线斜率为1,可求出参数![]() 的值,再对导函数
的值,再对导函数![]() 的零点进行分类讨论,即可求出函数
的零点进行分类讨论,即可求出函数![]() 的单调区间;(Ⅱ)由
的单调区间;(Ⅱ)由![]() ,构造辅助函数
,构造辅助函数![]() ,再对
,再对![]() 进行求导,讨论
进行求导,讨论![]() 的取值范围,利用函数单调性判断函数的最值,进而确定
的取值范围,利用函数单调性判断函数的最值,进而确定![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)∵![]() ∴
∴![]() ∴
∴![]() ,
,
∴![]() ,记
,记![]() ∴
∴![]() ,
,
当x<0时, ![]() 单减;
单减;
当x>0时,![]() 单增,
单增,
∴![]() ,
,
故![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增.
上单调递增.
(Ⅱ)∵![]() ,令
,令![]() ∴
∴![]() ,
,
当![]() 时,
时,![]() ∴
∴![]() 在
在![]() 上单增,∴
上单增,∴![]() .
.
i)当![]() 即
即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ∴
∴![]() 在
在![]() 上单增,
上单增,
∴![]() ,所以
,所以![]() .
.
ii)当![]() 即
即![]() 时,∵
时,∵![]() 在
在![]() 上单增,且
上单增,且![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 使
使![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,即
,即![]() 单减;
单减;
当![]() 时,
时,![]() ,即
,即![]() 单增.
单增.
∴![]() ,
,
∴![]() ,由
,由![]() ∴
∴![]() .
.
记![]() ,
,
∴![]() ∴
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ∴
∴![]() .
.
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在一个古典型(或几何概型)中,若两个不同随机事件![]() 、
、![]() 概率相等,则称
概率相等,则称![]() 和
和![]() 是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
①在同一个古典概型中,所有的基本事件之间都是“等概率事件”;
②若一个古典概型的事件总数为大于2的质数,则在这个古典概型中除基本事件外没有其他“等概率事件”;③因为所有必然事件的概率都是1,所以任意两个必然事件是“等概率事件”;
④随机同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”.
查看答案和解析>>
科目:高中数学 来源: 题型:
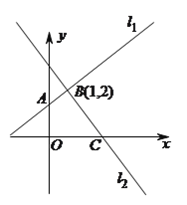
【题目】如图,经过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如果![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)试问是否总存在经过![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级举办团知识竞赛.![]() 、
、![]() 、
、![]() 、
、![]() 四个班报名人数如下:
四个班报名人数如下:
班别 |
|
|
|
|
人数 | 45 | 60 | 30 | 15 |
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(Ⅰ)求各班参加竞赛的人数;
(Ⅱ)若![]() 班每位参加竞赛的同学对每个题目答对的概率均为
班每位参加竞赛的同学对每个题目答对的概率均为![]() ,求
,求![]() 班恰好有2位同学获得奖品的概率;
班恰好有2位同学获得奖品的概率;
(Ⅲ)若这10个题目,小张同学只有2个答不对,记小张答对的题目数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an= ![]() (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= ![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个粮库要向A,B两镇运送大米,已知甲库可调出100 t大米,乙库可调出80 t大米,A镇需70 t大米,B镇需110 t大米.两库到两镇的路程和运费如下表:

这两个粮库各运往A,B两镇多少t大米,才能使总运费最省?此时总运费是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的线性回归方程,对于基本苗数56.7预报其有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求R2,并说明残差变量对有效穗的影响占百分之几.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com