
【题目】“现代五项”是由现代奥林匹克之父顾拜旦先生创立的运动项目,包含射击、击剑、游泳、马术和越野跑五项运动.已知甲、乙、丙共三人参加“现代五项”.规定每一项运动的前三名得分都分别为![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() ),选手最终得分为各项得分之和.已知甲最终得22分,乙和丙最终各得9分,且乙的马术比赛获得了第一名,则游泳比赛的第三名是
),选手最终得分为各项得分之和.已知甲最终得22分,乙和丙最终各得9分,且乙的马术比赛获得了第一名,则游泳比赛的第三名是
A. 甲 B. 乙 C. 丙 D. 乙和丙都有可能
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或下满6局时停止.设甲在每局中获胜的概率为p(p> ![]() ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 ![]() .
.
(1)求p的值;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F. 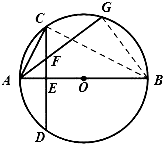
(1)求证:E、F、G、B四点共圆;
(2)若GF=2FA=4,求线段AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是BC的中点. 
(1)若E为B1C1的中点,求证:BE∥平面AC1D;
(2)若平面B1BCC1⊥平面ABC,且AB=AC,求证:平面AC1D⊥平面B1BCC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
(1)求函数f(x)的单调区间;
(2)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +lnx,其中a为实常数.
+lnx,其中a为实常数.
(1)讨论f(x)的单调性;
(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,若圆x2+y2=a2被直线x﹣y﹣
,若圆x2+y2=a2被直线x﹣y﹣![]() =0截得的弦长为2
=0截得的弦长为2
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点A、B为动直线y=k(x﹣1),k≠0与椭圆C的两个交点,问:在x轴上是否存在定点M,使得![]() 为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用a代表红球,b代表蓝球,c代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a)(1+b)的展开式1+a+b+ab表示出来,如:“1”表示一个球都不取、“a”表示取出一个红球,而“ab”表示把红球和蓝球都取出来,以此类推,下列各式中,其展开式可用来表示从3个无区别的红球、3个无区别的蓝球、2个有区别的黑球中取出若干个球,且所有蓝球都取出或都不取出的所有取法的是
①(1+a+a2+a3)(1+b3)(1+c)2
②(1+a3)(1+b+b2+b3)(1+c)2
③(1+a)3(1+b+b2+b3)(1+c2)
④(1+a3)(1+b)3(1+c+c2)
查看答案和解析>>
科目:高中数学 来源: 题型:
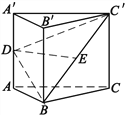
【题目】如图,正三棱柱![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一点,
上的一点,![]() .
.
(1)若![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)平面![]() 将棱柱
将棱柱![]() 分割为两个几何体,记上面一个几何体的体积为
分割为两个几何体,记上面一个几何体的体积为![]() ,下面一个几何体的体积为
,下面一个几何体的体积为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com