
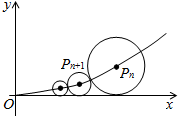
 在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).
在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).分析 (1)依题意,⊙Pn的半径${r_n}={y_n}={x_n}^2$,由于⊙Pn与⊙Pn+1彼此外切,可得|PnPn+1|=rn+rn+1,$\sqrt{{{({x_n}-{x_{n+1}})}^2}+{{({y_n}-{y_{n+1}})}^2}}={y_n}+{y_{n+1}}$.化简整理利用等差数列的通项公式即可得出.
(2)由(1)可得${x}_{n}=\frac{1}{2n-1}$,可得Sn,再利用“裂项求和”即可得出.
解答 (1)证明:依题意,⊙Pn的半径${r_n}={y_n}={x_n}^2$,
∵⊙Pn与⊙Pn+1彼此外切,
∴|PnPn+1|=rn+rn+1,∴$\sqrt{{{({x_n}-{x_{n+1}})}^2}+{{({y_n}-{y_{n+1}})}^2}}={y_n}+{y_{n+1}}$.
两边平方,化简得${({x_n}-{x_{n+1}})^2}=4{y_n}{y_{n+1}}$,即${({x_n}-{x_{n+1}})^2}=4x_n^2x_{n+1}^2$.
∵xn>xn+1>0,∴xn-xn+1=2xnxn+1,$⇒\frac{1}{{{x_{n+1}}}}-\frac{1}{x_n}=2(n∈{N_+})$.
∴数列$\left\{{\frac{1}{x_n}}\right\}$是等差数列.
(2)解:由题设,x1=1,∴$\frac{1}{x_n}=\frac{1}{x_1}+(n-1)•2⇒{x_n}=\frac{1}{2n-1}$.
${S_n}=π{r_n}^2=π{y_n}^2=π{x_n}^4=\frac{π}{{{{(2n-1)}^4}}}$.
${T_n}=\sqrt{S_1}+\sqrt{S_2}+…+\sqrt{S_n}$
=$\sqrt{π}[{1+\frac{1}{3^2}+\frac{1}{5^2}+…+\frac{1}{{{{(2n-1)}^2}}}}]$≤$\sqrt{π}[{1+\frac{1}{1•3}+\frac{1}{3•5}+…+\frac{1}{(2n-3)•(2n-1)}}]$
=$\sqrt{π}\left\{{1+\frac{1}{2}[{(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-3}-\frac{1}{2n-1})}]}\right\}$
=$\sqrt{π}[{1+\frac{1}{2}(1-\frac{1}{2n-1})}]$
=$\frac{{3\sqrt{π}}}{2}-\frac{{\sqrt{π}}}{2(2n-1)}<\frac{{3\sqrt{π}}}{2}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法、圆的性质及其面积计算公式,考查了变形能力、推理能力与计算能力,属于难题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
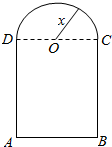 为迎接2015级新生,合肥一中暑期对教学楼窗户作加固,制作如图所示的窗户框架.窗户框架用料12m,下部为矩形,上部为半圆形,假设半圆半径为xm.
为迎接2015级新生,合肥一中暑期对教学楼窗户作加固,制作如图所示的窗户框架.窗户框架用料12m,下部为矩形,上部为半圆形,假设半圆半径为xm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com