
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,![]() ,点O为AD的中点,
,点O为AD的中点,![]() 且
且![]() .
.
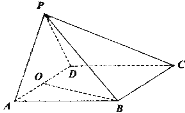
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求平面PBC与平面PAD所成二面角的正弦值.
,求平面PBC与平面PAD所成二面角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)连结OP,BD,先证![]() ,则
,则![]() ,设
,设![]() ,可表示OB,PO,由勾股定理可得
,可表示OB,PO,由勾股定理可得![]() ,从而根据线面垂直的判定定理证明结论;
,从而根据线面垂直的判定定理证明结论;
(2)根据条件证明![]() ,可得OA,OB,OP所在的直线两两互相垂直,故以OA,OB,OP所在直线为x轴,y轴,z轴建立坐标系,由
,可得OA,OB,OP所在的直线两两互相垂直,故以OA,OB,OP所在直线为x轴,y轴,z轴建立坐标系,由![]() 平面PAD,故可以取与
平面PAD,故可以取与![]() 平行的向量
平行的向量![]() 作为平面PAD的法向量,再利用空间向量法求出平面PBC的法向量
作为平面PAD的法向量,再利用空间向量法求出平面PBC的法向量![]() ,从而利用向量的夹角公式求得结果.
,从而利用向量的夹角公式求得结果.
(1)证明:连结OP,BD,因为底面ABCD为菱形,![]() ,
,
故![]() ,又O为AD的中点,故
,又O为AD的中点,故![]() .
.
在![]() 中,
中,![]() ,O为AD的中点,所以
,O为AD的中点,所以![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() .(也可通过
.(也可通过![]() 来证明
来证明![]() ),
),
又因为![]() ,
,![]() 平面PAD,
平面PAD,![]() 平面PAD,
平面PAD,
所以![]() 平面PAD;
平面PAD;
(2)因为![]() ,
,![]() ,
,
![]() ,
,![]() 平面POB,
平面POB,![]() 平面POB,
平面POB,
所以![]() 平面POB,又
平面POB,又![]() 平面POB,所以
平面POB,所以![]() .
.
由(1)得![]() 平面PAD,又
平面PAD,又![]() 平面PAD,故有
平面PAD,故有![]() ,又由
,又由![]() ,
,
所以OA,OB,OP所在的直线两两互相垂直.
故以O为坐标原点,以OA,OB,OP所在直线为x轴,y轴,z轴如图建系.
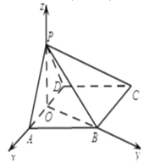
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 平面PAD,
平面PAD,
故可以取与![]() 平行的向量
平行的向量![]() 作为平面PAD的法向量.
作为平面PAD的法向量.
设平面PBC的法向量为![]() ,则
,则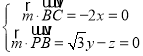 ,
,
令![]() ,所以
,所以![]() .
.
设平面PBC与平面PAD所成二面角为θ,则![]() ,
,
则![]() ,所以平面PBC与平面PAD所成二面角的正弦值为
,所以平面PBC与平面PAD所成二面角的正弦值为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形仓库用于贮藏食盐已建的仓库的底面直径为![]() ,高
,高![]() ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大![]() (高不变);二是高度增加
(高不变);二是高度增加![]() ,(底面直径不变).
,(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为![]() ,且甲、乙两人是否答对每个试题互不影响.
,且甲、乙两人是否答对每个试题互不影响.
(1)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;
(2)若答对一题得5分,答错或不答得0分,记乙答题的得分为![]() ,求
,求![]() 的分布列及数学期望和方差.
的分布列及数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点,且AA1=![]() AD.
AD.
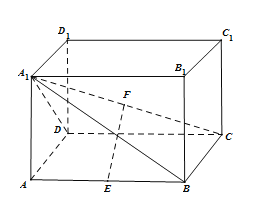
(1)求直线EF与平面ABCD所成角的大小;
(2)若EF=![]() AB,求二面角B-A1C-D的余弦值.
AB,求二面角B-A1C-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在交通工程学中,常作如下定义:交通流量![]() (辆/小时):单位时间内通过道路上某一横断面的车辆数;车流速度
(辆/小时):单位时间内通过道路上某一横断面的车辆数;车流速度![]() (千米/小时):单位时间内车流平均行驶过的距离;车流密度
(千米/小时):单位时间内车流平均行驶过的距离;车流密度![]() (辆/千米):单位长度道路上某一瞬间所存在的车辆数. 一般的,
(辆/千米):单位长度道路上某一瞬间所存在的车辆数. 一般的,![]() 和
和![]() 满足一个线性关系,即
满足一个线性关系,即![]() (其中
(其中![]() 是正数),则以下说法正确的是
是正数),则以下说法正确的是
A. 随着车流密度增大,车流速度增大
B. 随着车流密度增大,交通流量增大
C. 随着车流密度增大,交通流量先减小,后增大
D. 随着车流密度增大,交通流量先增大,后减小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com