
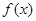 和
和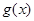 的图像关于原点对称,且
的图像关于原点对称,且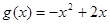 .
.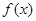 的解析式;
的解析式;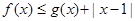 ;
;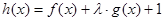 在区间
在区间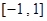 上是增函数,求实数
上是增函数,求实数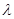 的取值范围.
的取值范围. ;(2) 解集为
;(2) 解集为 ;(3)
;(3)  .
. ,求出这点的对称点的坐标
,求出这点的对称点的坐标 ,当然这里
,当然这里 是用
是用 表示的式子,然后把点
表示的式子,然后把点 代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3)
代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3)  ,这是含参数的二次函数,解题时,首先对二次项系数
,这是含参数的二次函数,解题时,首先对二次项系数 分类,即分二次项系数
分类,即分二次项系数 为0,不为0,其中
为0,不为0,其中 不为0还要分为是正数,还是负数进行讨论,在二次项系数
不为0还要分为是正数,还是负数进行讨论,在二次项系数 不为0时,只要讨论其对称轴与给定区间的关系就能求得结论.
不为0时,只要讨论其对称轴与给定区间的关系就能求得结论. 是函数
是函数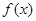 图像上任一点,则
图像上任一点,则 关于原点对称的点
关于原点对称的点 在函数
在函数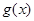 的图像上, (1分)
的图像上, (1分) ,故
,故 . (2分)
. (2分)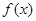 的解析式是
的解析式是 . (1分)
. (1分)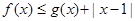 ,得
,得 , (1分)
, (1分) . (1分)
. (1分) 时,有
时,有 ,△
,△ ,不等式无解; (1分)
,不等式无解; (1分) 时,有
时,有 ,
, ,解得
,解得 . (2分)
. (2分)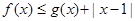 的解集为
的解集为 . (1分)
. (1分) . (1分)
. (1分) 时,
时, 在区间
在区间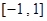 上是增函数,符合题意. (1分)
上是增函数,符合题意. (1分) 时,函数
时,函数 图像的对称轴是直线
图像的对称轴是直线 . (1分)
. (1分) 在区间
在区间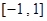 上是增函数,所以,
上是增函数,所以, 时,
时, ,函数
,函数 图像开口向上,故
图像开口向上,故 ,
, ; (1分)
; (1分) 时,
时, ,函数
,函数 图像开口向下,故
图像开口向下,故 ,解得
,解得 . (1分)
. (1分)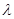 的取值范围是
的取值范围是 . (1分)
. (1分)

科目:高中数学 来源:不详 题型:解答题
 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元; 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费. (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
 ;
; 的图像关于直线
的图像关于直线 对称;
对称; 值域为
值域为 ;
; 在区间
在区间 上单调递增.
上单调递增.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com