
【题目】我们要计算由抛物线![]() ,x轴以及直线
,x轴以及直线![]() 所围成的区域的面积S,可用x轴上的分点
所围成的区域的面积S,可用x轴上的分点![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、1将区间
、1将区间![]() 分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线
分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线![]() 上,这些矩形的高分别为
上,这些矩形的高分别为![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,矩形的底边长都是
,矩形的底边长都是![]() ,设所有这些矩形面积的总和为
,设所有这些矩形面积的总和为![]() ,为求S,只须令分割的份数n无限增大,
,为求S,只须令分割的份数n无限增大,![]() 就无限趋近于S,即
就无限趋近于S,即![]() .
.
(1)求数列![]() 的通项公式,并求出S;
的通项公式,并求出S;
(2)利用相同的思想方法,探求由函数![]()
![]() 的图象,x轴以及直线
的图象,x轴以及直线![]() 和
和![]() 所围成的区域的面积T.
所围成的区域的面积T.
科目:高中数学 来源: 题型:
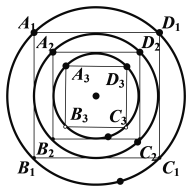
【题目】如图,内接于圆![]() 的正方形
的正方形![]() 边长为1,圆
边长为1,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,···,正方形
,···,正方形![]() 内接于圆
内接于圆![]() ,圆
,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,由此无穷个步骤进行下去记圆
,由此无穷个步骤进行下去记圆![]() 的面积记作
的面积记作![]() ,记正方形
,记正方形![]() 的面积记作
的面积记作![]() .
.
(1)求![]() 的值
的值
(2)记![]() 的所有项和为
的所有项和为![]() ,
,![]() 的所有项和为
的所有项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中
①.对于命题![]() :存在
:存在![]() ,则
,则![]() :
:![]() ;
;
②.命题“若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数”的逆命题为假命题;
上是增函数”的逆命题为假命题;
③.若![]() 为真命题,则
为真命题,则![]() 均为真命题;
均为真命题;
④.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”.
”.
错误的是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】社区服务是高中学生社会实践活动的一个重要内容,汉中某中学随机抽取了100名男生、100名女生,了解他们一年参加社区服务的时间,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
(单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
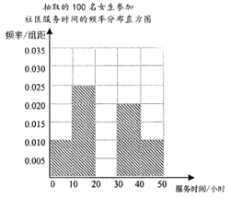
(1)完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
(2)按高中综合素质评价的要求,高中学生每年参加社区服务的时间不少于20个小时才为合格,根据上面的统计图表,完成抽取的这200名学生参加社区服务时间合格与性别的列联表,并判断是否有![]() 以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
(3)用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况,并以频率作为概率.
(i)求全市高中学生参加社区服务时间不少于30个小时的人数.
(ⅱ)对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其
,其![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以平面直角坐标系的原点为极点,
),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 被圆截得的弦长为
被圆截得的弦长为![]() 时,求
时,求![]() 的值.
的值.
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() ,垂足为
,垂足为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求△
,求△![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com